Appearance
3.5.4 几何变换和坐标变换
1. 变换
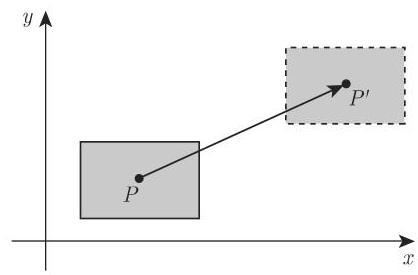
变换刻画的是平面上或空间中对象的位置或形式的改变. 有两种考虑, 它们相互间有密切的联系 [3.22]. 第一种情形是在固定坐标系中对点或对象进行变换. 这称为几何变换(参见第 308 页 3.5.4.1, 第 314 页 3.5.4.5, 1.).
第二种情形中则是对象保持不变, 而对与对象关联的坐标系进行变换. 经过这种坐标变换后 (参见第 311 页 3.5.4.3, 第 315 页 3.5.4.5, 2.), 发生改变的不是对象而是其坐标表示. 在解题时, 其中的一个可能比另一个更适合.
2. 应用领域
在其本身的对象坐标系中刻画建筑构件.
相互关联的零件的运动描述 (例如, 机器人).
再现三维对象的二维投影.
在计算机图形学或计算机动画中刻画运动和变形.
3.5.4.1 几何 2D 变换
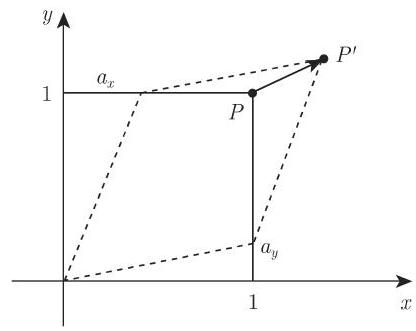
1. 平移
由笛卡儿坐标
如果坐标由列向量刻画, 则新坐标的变换公式和逆变换公式为
2. 围绕原点的旋转
在旋转时对象围绕原点旋转
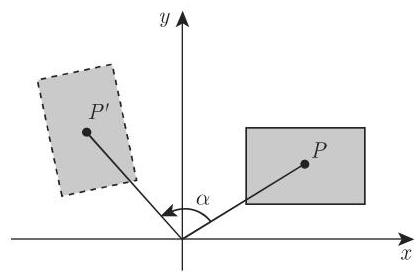
(3.432) 的矩阵形式为
这一变换的逆对应于旋转
(3.433b)
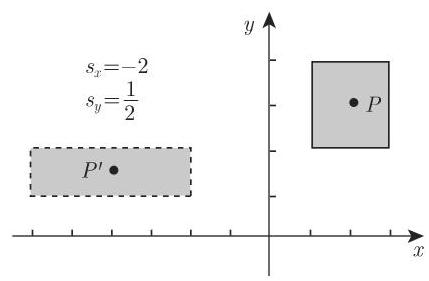
3. 关于原点的缩放变换
在缩放变换时坐标分别乘以
给出. 这一变换的矩阵形式及其逆为
缩放变换导致变换对象大小的改变. 一个正的乘数
特殊情形的缩放变换:
关于
轴的反射: . 关于
轴的反射: . 关于原点的反射:
.
4. 剪切变换
在剪切变换时每个坐标的值的改变与另一个坐标成比例. 这一变换的公式为
这一变换的矩阵形式 (符号
图 3.204 显示的是剪切变换的一个例子.
5. 变换的性质
上面引入的变换是仿射变换,即变换点
评论 这些变换保持共线性和平行性, 即直线变换成直线, 平行线的像是平行线. 而且平移、旋转和反射是保距和保角映射.
3.5.4.2 齐次坐标、矩阵表示
尽管旋转变换、缩放变换和剪切变换中的坐标改变能够用乘以
在以下将固定
平移矩阵、旋转矩阵、缩放矩阵和剪切矩阵为
旋转矩阵
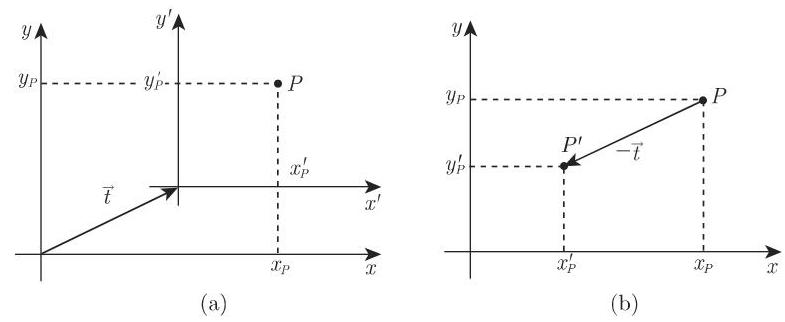
3.5.4.3 坐标变换
在几何变换中, 关于对象的变换是在固定坐标系中进行的. 而坐标变换给出的是固定对象在两个不同坐标系中坐标表示之间的关系.
两种类型变换之间的关系显示在图 3.205 中. 如果借助向量
同样的结果对于旋转和缩放也成立. 因此, 坐标系的变换等价于对象的逆变换.
由平移、旋转或缩放导致的坐标变换可以由
这样,所有的基本变换都可以用一个
3.5.4.4 变换的复合
复杂的几何变换可以通过不同基本变换的组合来实现. 设有矩阵
类似地, 相反的变换
于是,作为对一个点进行
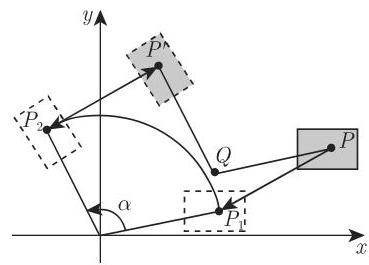
每个仿射变换可以作为一连串平移、旋转和缩放的复合给出, 甚至剪切也可以作为一次旋转
(1) 将
(2)围绕原点旋转:
(3) 将原点平移回
这些变换的单个步骤序列见图 3.206. 经由
- 关于由方程
给出的一条直线的反射:
(1)将该直线平移通过原点:
(2) 顺时针旋转该直线直到它与
(3) 关于
(4) 往回旋转
(5) 将该直线平移回原来的位置:
利用著名的三角关系
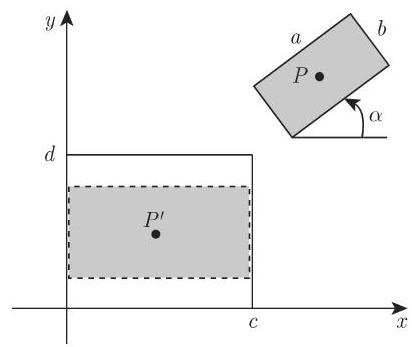
- 所裁边长为
和 的矩形到宽为 且高为 的窗口中相似矩形的完全中心变换 (图 3.207). 基本变换序列:
(1) 将
(2)顺时针旋转角
(3) 按因子
(4) 将原点移到窗口中心:
3.5.4.5 3D 变换
三维空间中几何变换和坐标变换的数学刻画基于已在
1. 几何变换
点
(3.450)
基本变换的变换矩阵是
关于原点的缩放
围绕
围绕
围绕
平行于
对于正的
(3.457)
2. 坐标变换
类似于二维的情形, 坐标系的变换对于点的坐标表示来说具有和逆几何变换 (参见第 311 页 3.5.4.3) 相同的效果. 因此, 变换矩阵是
在实际应用中常会发生从一个右手笛卡儿坐标系到另一个笛卡儿坐标系一个特定的变换被取代的情况. 最初的一个常被称为世界坐标系, 而另一个则被称为局部或对象坐标系. 如果在世界坐标系中给出局部坐标系的原点
给出.
如果点
如果
给出.
- 确定围绕通过点
和 具有方向向量 , 的直线旋转 角的旋转矩阵. 易选取 和 使它们之间的距离为一个单位,因此 是一个单位向量. 首先将该直线变换成坐标系的 轴. 接下来,围绕 轴旋转 角. 最后将直线变换回原来的直线. 图 3.208 显示将特定直线变换成 轴是如何进行的. 它包括以下步骤:
(1) 将
(2) 围绕
点
(3) 围绕
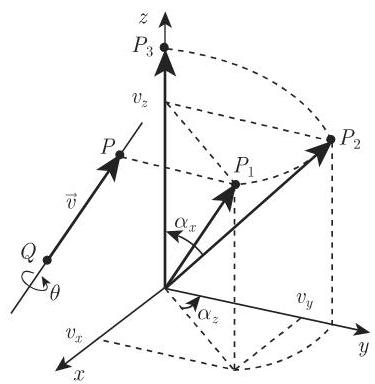
设
将
在第 386 页 4.4 中我们将利用四元数的性质给出另一种方法来刻画旋转矩阵.
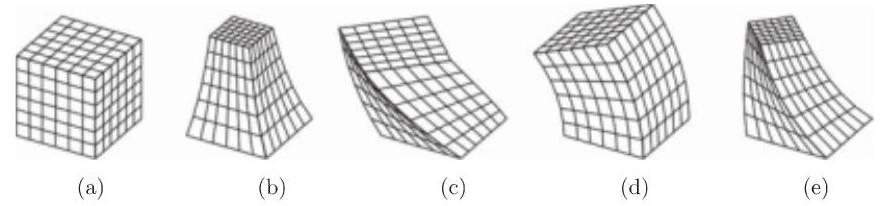
3.5.4.6 形变变换
在第 314 页 3.5.4.5 讨论的仿射变换改变了对象的位置并产生了沿给定方向的拉伸或压缩. 如果变换矩阵
1. 收缩
这一变换是缩放的推广. 在沿
函数
2. 围绕
这一变换是围绕
函数
3. 围绕
弯曲时旋转角沿与旋转轴垂直的方向改变. 变换矩阵具有下面的形式:
图 3.209(d) 显示的是单位立方体以
像仿射变换一样, 这些形变可以进行系列应用. 图 3.209(e) 中的对象是单位立方体先收缩后扭曲的结果.