8.3.4 线积分与积分路径无关

线积分与积分路径无关的条件也称为全微分的可积性.

8.3.4.1 二维情况

设 $P$ 和 $Q$ 是定义在单连通区域上的连续函数,若积分

$$\begin{array}{}\text{(8.124)}& {\int }_{\left(C\right)}\left[P\left(x,y\right)\mathrm{d}x+Q\left(x,y\right)\mathrm{d}y\right]\end{array}$$

仅与积分路径的起点 $A$ 和终点 $B$ 有关,而与连接这两点的曲线无关,即对任意 $A$ , $B$ 及积分路径 $ACB$ 与 $ADB$ (图 8.27),都有等式

$$\begin{array}{}\text{(8.125)}& {\int }_{\stackrel{⏜}{ACB}}\left(P\mathrm{d}x+Q\mathrm{d}y\right)={\int }_{\stackrel{⏜}{ADB}}\left(P\mathrm{d}x+Q\mathrm{d}y\right),\end{array}$$

以上成立的充分必要条件为存在二元函数 $U\left(x,y\right)$ ,其全微分是线积分的被积函数:

$$\begin{array}{}\text{(8.126a)}& P\mathrm{d}x+Q\mathrm{d}y=\mathrm{d}U\end{array}$$

即

$$\begin{array}{}\text{(8.126b)}& P=\frac{\partial U}{\partial x},Q=\frac{\partial U}{\partial y}.\end{array}$$

函数 $U\left(x,y\right)$ 是全微分 (8.126a) 的原函数. 在物理学中,原函数 $U\left(x,y\right)$ 是向量场的势能 (参见第 941 页 13.3.1.6,4.).

8.3.4.2 原函数的存在性

原函数存在的充分必要条件,即表达式 $P\mathrm{d}x+Q\mathrm{d}y$ 可积的充要条件为偏导数

$$\begin{array}{}\text{(8.127)}& \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\end{array}$$

且偏导数连续.

8.3.4.3 三维情况

与二维的情况类似, 积分

$$\begin{array}{}\text{(8.128)}& \int \left[P\left(x,y,z\right)\mathrm{d}x+Q\left(x,y,z\right)\mathrm{d}y+R\left(x,y,z\right)\mathrm{d}z\right]\end{array}$$

与积分路径无关的条件是: 存在原函数 $U\left(x,y,z\right)$ ,满足

$$\begin{array}{}\text{(8.129a)}& P\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z=\mathrm{d}U,\end{array}$$

即

$$\begin{array}{}\text{(8.129b)}& P=\frac{\partial U}{\partial x},Q=\frac{\partial U}{\partial y},R=\frac{\partial U}{\partial z}.\end{array}$$

可积条件是若偏导数连续, 则它们同时满足如下三个方程

$$\begin{array}{}\text{(8.129c)}& \frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y},\frac{\partial R}{\partial x}=\frac{\partial P}{\partial z},\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}.\end{array}$$

$◼$ 功 $W$ (参见第 670 页 8.2.2.3,2.) 可定义为力 $\overrightarrow{F}\left(\overrightarrow{r}\right)$ 与位移 $\overrightarrow{s}$ 的点积. 在守恒场中功仅与位置 $\overrightarrow{r}$ 有关,而与速度 $\overrightarrow{v}$ 无关. 设 $\overrightarrow{F}=P{\overrightarrow{e}}_x+Q{\overrightarrow{e}}_y+R{\overrightarrow{e}}_z=\mathrm{grad}V$ , $\mathrm{d}\overrightarrow{s}=\mathrm{d}x{\overrightarrow{e}}_x+\mathrm{d}y{\overrightarrow{e}}_y+\mathrm{d}z{\overrightarrow{e}}_x$ ,则势能 $V\left(\overrightarrow{r}\right)$ 满足关系 (8.129a) 和 (8.129b),且有等式 (8.129c) 成立. 功与点 $P_1$ 和 $P_2$ 间的积分路径无关:

$$\begin{array}{}\text{(8.130)}& W={\int }_{P_1}^{P_2}\overrightarrow{F}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{s}={\int }_{P_1}^{P_2}\left[P\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z\right]=V\left(P_2\right)-V\left(P_1\right).\end{array}$$

8.3.4.4 原函数的确定

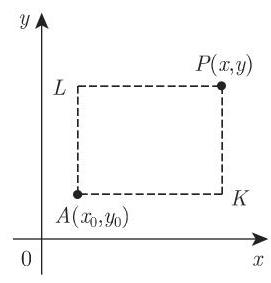
1. 二维情况 (图 8.28)

若满足可积条件 (8.127), 则在 (8.127) 成立的区域内, 沿着连接任意固定点 $A\left(x_0,y_0\right)$ 和动点 $P\left(x,y\right)$ 的积分路径,都有原函数 $U\left(x,y\right)$ 等于线积分

$$\begin{array}{}\text{(8.131)}& U={\int }_{\stackrel{⏜}{AP}}\left(P\mathrm{d}x+Q\mathrm{d}y\right)\end{array}$$

事实上, 为方便起见, 可在 (8.127) 成立的区域内选择平行于坐标轴的积分路径, 即折线 $AKP$ 或 $ALP$ ,故此存在两个计算原函数和全微分的公式:

$$\begin{array}{}\text{(8.132a)}& U=U\left(x_0,y_0\right)+{\int }_{\overline{AK}}+{\int }_{\overline{KP}}=C+{\int }_{x_0}^{x}P\left(\xi ,y_0\right)\mathrm{d}\xi +{\int }_{y_0}^{y}Q\left(x,\eta \right)\mathrm{d}\eta ,\end{array}$$$$\begin{array}{}\text{(8.132b)}& U=U\left(x_0,y_0\right)+{\int }_{\overline{AL}}+{\int }_{\overline{LP}}=C+{\int }_{y_0}^{y}Q\left(x_0,\eta \right)\mathrm{d}\eta +{\int }_{x_0}^{x}P\left(\xi ,y\right)\mathrm{d}\xi ,\end{array}$$

其中 $C$ 为任意常数.

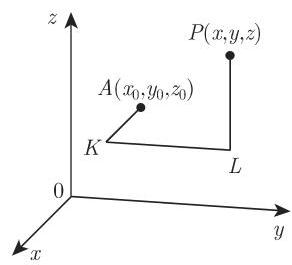
2. 三维情况 (图 8.29)

若满足条件 (8.129c),由积分路径 $AKLP$ ,可得原函数计算公式:

$$U=U\left(x_0,y_0,z_0\right)+{\int }_{\overline{AK}}+{\int }_{\overline{KL}}+{\int }_{\overline{LP}}$$$$={\int }_{x_0}^{x}P\left(\xi ,y_0,z_0\right)\mathrm{d}\xi +{\int }_{y_0}^{y}Q\left(x,\eta ,z_0\right)\mathrm{d}\eta +{\int }_{z_0}^{z}R\left(x,y,\xi \right)\mathrm{d}\xi +C\left(C\text{ 为任意常数 }\right).$$

(8.133)

沿着平行坐标轴的方向还有其他 5 条可能的积分路径, 由此又可进一步得到 5 个公式.

$◼\mathbf{A}$: $P\mathrm{d}x+Q\mathrm{d}y=-\frac{y\mathrm{d}x}{x^2+y^2}+\frac{x\mathrm{d}y}{x^2+y^2}$ . 满足条件 (8.129c): $\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}=$ $\frac{y^2-x^2}{{(x^2+y^2)}^2}$ . 利用(8.132b),令 $x_0=0,y_0=1$ (因为函数 $P$ 和 $Q$ 在点(0,0)不连续,故不选 $x_0=0,y_0=0)$ ,得

$$U={\int }_1^y\frac{0\cdot \mathrm{d}\eta }{0^2+{\eta }^2}+{\int }_0^x\frac{-y\mathrm{d}\xi }{{\xi }^2+y^2}+U\left(0,1\right)=-\arctan \frac{x}{y}+C=\arctan \frac{y}{x}+C_1.$$

$◼\mathbf{B}$: $P\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z=z\left(\frac{1}{x^{2}y}-\frac{1}{x^2+z^2}\right)\mathrm{d}x+\frac{z}{x{y}^2}\mathrm{d}y+\left(\frac{x}{x^2+z^2}-\frac{1}{xy}\right)\mathrm{d}z$ . 满足条件 (8.129c),利用 (8.133),令 $x_0=1,y_0=1,z_0=0$ ,得

$$U={\int }_1^{x}0\cdot \mathrm{d}\xi +{\int }_1^{y}0\cdot \mathrm{d}\eta +{\int }_0^z\left(\frac{x}{x^2+{\zeta }^2}-\frac{1}{xy}\right)\mathrm{d}\zeta +C=\arctan \frac{z}{x}-\frac{z}{xy}+C.$$

8.3.4.5 沿闭曲线的零值积分

若积分曲线为一闭曲线,(8.127) 成立,且该闭曲线内部不含使 $P,Q,\frac{\partial P}{\partial y},\frac{\partial Q}{\partial x}$ 不连续或没定义的点,则 $P\mathrm{d}x+Q\mathrm{d}y$ 的线积分为 0 .

注 当不满足上述条件时, 积分值也可等于 0 , 但是这个值只能是进行相应计算后得到的.