14.2.1 定积分和不定积分

14.2.1.1 复平面中积分的定义

1. 复定积分

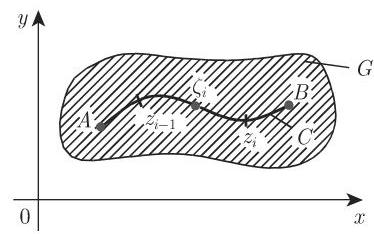
假设 $f\left(z\right)$ 在一个域 $G$ 中是连续的,并且连接点 $A$ 和 $B$ 的曲线 $C$ 完全在 $G$ 中. 曲线 $C$ 被任意分点 $z_i$ 分为 $n$ 个子弧段 (图 14.33).

在每个子弧段中选取一个点 ${\zeta }_i$ ,并形成和式

$$\begin{array}{}\text{(14.33a)}& \sum _{i=1}^{n}f\left({\zeta }_i\right)\mathrm{\Delta }{z}_i,\text{ 其中 }\mathrm{\Delta }{z}_i=z_i-z_{i-1}.\end{array}$$

如果当 $\mathrm{\Delta }{z}_i\to 0$ 以及 $n\to \mathrm{\infty }$ 时,与诸点 $z_i$ 和 ${\zeta }_i$ 的选取无关地存在极限

$$\begin{array}{}\text{(14.33b)}& \underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^{n}f\left({\zeta }_i\right)\mathrm{\Delta }{z}_i\end{array}$$

则此极限被称为沿着连接点 $A$ 和 $B$ 的曲线 $C$ 的复定积分 (definite complex inte-

gral)

$$\begin{array}{}\text{(14.33c)}& I={\int }_{\stackrel{⏜}{AB}}f\left(z\right)\mathrm{d}z=\left(C\right){\int }_A^{B}f\left(z\right)\mathrm{d}z.\end{array}$$

该积分的值通常依赖于积分的路径.

2. 复不定积分

如果定积分不依赖于积分路径 (参见第 976 页 14.2.2), 则成立

$$\begin{array}{}\text{(14.34)}& F\left(z\right)=\int f\left(z\right)\mathrm{d}z+C,\text{ 其中 }{F}^{\prime }\left(z\right)=f\left(z\right).\end{array}$$

这里 $C$ 是积分常数,一般而言,它是复的. $F\left(z\right)$ 被称为复不定积分 (indefinite complex integral). 一个复变量初等函数的不定积分可以用一个实变量相应的初等函数的积分公式来计算.

$◼\mathbf{A}$: $\int \sin z\mathrm{d}z=-\cos z+C$ . $◼$ B: $\int {\mathrm{e}}^z\mathrm{d}z={\mathrm{e}}^z+C$ .

3. 复定积分和复不定积分的关系

如果函数 $f\left(z\right)$ 是解析的 (参见第 954 页 14.1.2.1),并且有一个不定积分,则其定积分和不定积分之间的关系为

$$\begin{array}{}\text{(14.35)}& {\int }_{\stackrel{⏜}{AB}}f\left(z\right)\mathrm{d}z={\int }_A^{B}f\left(z\right)\mathrm{d}z=F\left(z_B\right)-F\left(z_A\right).\end{array}$$

14.2.1.2 复积分的性质和求值

1. 与第二型线积分的比较

复定积分与第二型线积分 (参见第 687 页 8.3.2) 有相同的性质:

a) 颠倒积分路径的方向, 积分改变符号.

b) 把积分路径分解成几个部分, 总积分值等于这些部分积分值之和.

2. 积分值的估计

如果在积分路径 $\stackrel{⏜}{AB}$ 的每个点 $z$ 处函数 $f\left(z\right)$ 的绝对值不超过一个正数 $M$ , 并且 $\stackrel{⏜}{AB}$ 有长度 $s$ ,则

$$\begin{array}{}\text{(14.36)}& \left|{\int }_{\stackrel{⏜}{AB}}f\left(z\right)\mathrm{d}z\right|\le Ms.\end{array}$$

3. 用参数表示的复积分值的求值

如果用下述形式给出积分路径 $\stackrel{⏜}{AB}$ (或曲线 $C$ )

$$\begin{array}{}\text{(14.37)}& x=x\left(t\right),y=y\left(t\right),\end{array}$$

其中 $x$ 和 $y$ 是 $t$ 的可微函数,并且起始点和终点的 $t$ 值是 $t_A$ 和 $t_B$ ,那么可以用两个实积分来计算复定积分. 把被积函数的实部和虚部分开, 则复积分为

$$\text{(C)}{\int }_A^{B}f\left(z\right)\mathrm{d}z={\int }_A^B\left(u\mathrm{d}x-v\mathrm{d}y\right)+\mathrm{i}{\int }_A^B\left(v\mathrm{d}x+u\mathrm{d}y\right)$$$$={\int }_{t_A}^{t_B}\left[u\left(t\right)x^{\prime }\left(t\right)-v\left(t\right)y^{\prime }\left(t\right)\right]\mathrm{d}t$$$$\begin{array}{}\text{(14.38a)}& +\mathrm{i}{\int }_{t_A}^{t_B}\left[v\left(t\right)x^{\prime }\left(t\right)+u\left(t\right)y^{\prime }\left(t\right)\right]\mathrm{d}t,\end{array}$$

其中

$$\begin{array}{}\text{(14.38b)}& f\left(z\right)=u\left(x,y\right)+\mathrm{i}v\left(x,y\right),z=x+\mathrm{i}y.\end{array}$$

记号 $\left(C\right){\int }_A^{B}f\left(z\right)\mathrm{d}z$ 意味着定积分是沿着在 $A$ 和 $B$ 之间的曲线 $C$ 而被计算的. 记号 ${\int }_{\stackrel{⏜}{AB}}f\left(z\right)\mathrm{d}z$ 也经常被用到,它有相同的含义.

$I={\int }_{\left(C\right)}{(z-z_0)}^n\mathrm{d}z\left(n\in \mathbb{Z}\right)$ . 令曲线 $C$ 是半径为 $r_0$ ,圆心为 $z_0$ 的圆周: $x=x_0+r_0\cos t,y=y_0+r_0\sin t$ ,其中 $0\le t\le 2\pi$ . 对于曲线 $C$ 上的每个点 $z$ : $z=x+\mathrm{i}y=z_0+r_0\left(\cos t+\mathrm{i}\sin t\right)$ ,有 $\mathrm{d}z=r_0\left(-\sin t+\mathrm{i}\cos t\right)\mathrm{d}t$ . 根据棣莫弗 (de Moivre) 公式,在代入这些值并变换后即得 $I=r_0^{n+1}{\int }_0^{2\pi }\left(\cos nt+\mathrm{i}\sin nt\right)(-\sin t+$$\mathrm{i}\cos t)\mathrm{d}t=r_0^{n+1}{\int }_0^{2\pi }\left[\mathrm{i}\cos \left(n+1\right)t-\sin \left(n+1\right)t\right]\mathrm{d}t=\{\begin{array}{ll}0,& n\ne -1,\\ 2\pi \mathrm{i},& n=-1.\end{array}$

4. 与积分路径的无关性

假设在一个单连通区域中定义了一个复变量的一个函数 $f\left(z\right)$ . 该函数的积分 (14.33c) 可以与连接两个固定点 $A\left(z_A\right)$ 和 $B\left(z_B\right)$ 的路径无关. 一个充要条件是: 函数 $f\left(z\right)$ 在此区域中是解析的,即函数 $u$ 和 $v$ 满足柯西-黎曼微分方程 (参见第 955 页 (14.4)). 此时等式 (14.35) 也成立. 如果一个区域由一条简单闭曲线所围, 那么这个区域是单连通的 (simply connected).

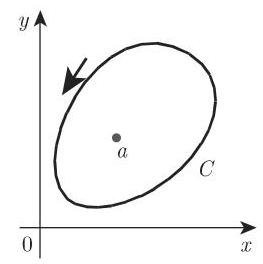
5. 沿着一条闭曲线的复积分

假设在一个单连通区域 $G$ 中函数 $f\left(z\right)$ 是解析的. 沿着 $G$ 的边界闭曲线 $C$ 积分函数 $f\left(z\right)$ ,根据柯西积分定理,这个积分的值为零 (参见第 976 页 14.2.2):

$$\begin{array}{}\text{(14.39)}& \left(C\right)\oint f\left(z\right)\mathrm{d}z=0.\end{array}$$

如果 $f\left(z\right)$ 在这个区域中有奇点,则用留数定理 (参见第 984 页 14.3.5.5),或由公式 (14.38a) 来计算积分.

在 $z=a$ 处有一个奇点的函数 $f\left(z\right)=\frac{1}{z-a}$ 对于以逆时针方向围绕 $a$ 的闭曲线 $C$ (图 14.34) 有积分值 $\left(C\right)\oint \frac{1}{z-a}\mathrm{d}z={2\pi \mathrm{i}\mathrm{Res}f\left(z\right)|}_{z=a}=2\pi \mathrm{i}$ .