3.4.1 球面几何学的基本概念

3.4.1.1 球面上的曲线、弧和角

1. 球面曲线、大圆和小圆

球面上的曲线称为球面曲线. 重要的球面曲线有大圆和小圆. 它们是穿过球的平面, 即所谓的截割平面截出的相交圆 (图 3.81).

如果半径为 $R$ 的球被与球心 $O$ 距离为 $h$ 的平面 $K$ 所截,则相交圆的半径 $r$ 满足

$$\begin{array}{}\text{(3.174)}& r=\sqrt{R^2-h^2}\left(0\le h\le R\right).\end{array}$$

当 $h=0$ 时,截割平面穿过球心, $r$ 取最大可能的值. 在这一情形,平面 $\mathrm{\Gamma }$ 中的相交圆 $g$ 称为大圆. 任何其他的相交圆都有 $0<h<R$ ,称为小圆,例如图 3.81 中的圆 $k$ . 当 $h=R$ 时平面 $K$ 和球只有一个公共点. 这时它称为切平面.

在地球上,赤道和子午线及其相对子午线——它们是子午线关于地球自转轴的反射 —— 表示大圆. 平行的纬线是小圆 (参见第 215 页 3.4.1.2,1.).

2. 球面距离

通过球面上不是相对点 (即它们不是同一直径的端点) 的两点 $A$ 和 $B$ ,可以画出无穷多个小圆,但仅有一个大圆 (和大圆 $g$ 所在平面). 考虑通过 $A$ 和 $B$ 的两个小圆 $k_1,k_2$ 并将它们旋转入通过 $A$ 和 $B$ 的大圆平面中 (图 3.82). 大圆具有最大的半径,从而有最小的曲率. 因此大圆较短的弧就是 $A$ 和 $B$ 之间的最短连线. 它也是球面上 $A,B$ 两点之间的最短连线,称为球面距离.

3. 测地线

测地线是曲面上两点之间的最短连线 (参见第 359 页 3.6.3.6).

$◼$ 平面上的直线, 球面上的大圆都是测地线 (也见第 215 页 3.4.1.2,1.).

4. 球面距离的度量

两点的球面距离可以表示成长度, 也可以表示成角度 (图 3.83).

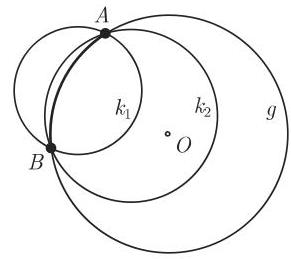
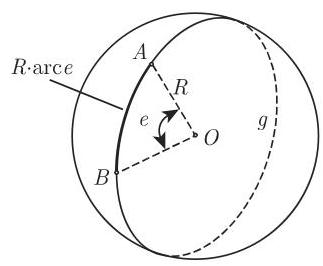
(1) 作为角度的球面距离 是在球心 $O$ 处所测的半径 $\overline{OA}$ 和 $\overline{OB}$ 之间的角. 这个角唯一确定了该球面距离, 以下将用小写拉丁字母表示它. 这一记号可以用在球心处或大圆弧上.

(2) 作为长度的球面距离 是 $A$ 和 $B$ 之间大圆弧的长. 我们用 $\stackrel{⏜}{AB}$ (弧 $AB$ ) 来标记.

(3)角度与长度之间的换算 可以用以下公式来做:

$$\begin{array}{}\text{(3.175a)}& \stackrel{⏜}{AB}=R\mathrm{arc}e=R\frac{e}{\varrho },\end{array}$$$$\begin{array}{}\text{(3.175b)}& e=\stackrel{⏜}{AB}\frac{\varrho }{R}\end{array}$$

这里 $e$ 表示用度给出的角, arc $e$ 表示用弧度给出的角 (参见第 170 页 3.1.1.5 弧度). 换算因子 $\varrho$ 等于

$$\begin{array}{}\text{(3.175c)}& \varrho =1\mathrm{rad}=\frac{{180}^{\circ }}{\pi }={57.2958}^{\circ }={3438}^{\prime }={206265}^{\prime \prime }.\end{array}$$

距离作为长度和角度来确定是等价的, 但在球面三角学中球面距离大多数情况下是以角度给出的.

$◼\mathbf{A}$:对于地球表面的球面计算通常考虑和克拉索夫斯基(Krassowski)双轴参考椭球同样体积的一个球. 该地球半径是 $R=6371.110\mathrm{km}$ ,因此有 $1^{\circ }\stackrel{\wedge }{=}111.2\mathrm{km}$ , $1^{\prime }=1853.3\mathrm{m}=1$ 旧海里. 今天 $1\mathrm{n}$ mile $=1852\mathrm{m}$ .

$◼\mathbf{B}$: 德累斯顿与圣彼得堡之间的球面距离是 $\stackrel{⏜}{AB}=1433\mathrm{km}$ 或

$$e=\frac{1433\mathrm{km}}{6371\mathrm{km}}{57.3}^{\circ }={12.89}^{\circ }={12}^{\circ }{53}^{\prime }.$$

5. 交叉角、航向角、方位角

两条球面曲线之间的交叉角是在交点 $P_1$ 处它们的切线之间的夹角. 如果其中之一是子午线,那么与从 $P_1$ 点起朝北的曲线段形成的交叉角 $\alpha$ 在导航中称为航向角. 为了区别偏向东的曲线和偏向西的曲线, 按照图 3.84(a), (b) 指派给航向角一个符号,并将其限制在区间 $-{90}^{\circ }<\alpha \le {90}^{\circ }$ 内. 因此航向角是一个有向角,即它具有符号. 就其含义来说, 它与曲线的定向无关.

如图 3.84(c) 从 $P_1$ 到 $P_2$ 的曲线的定向可以用方位角 $\delta$ 来描述: 它是通过 $P_1$ 的子午线的北半部分与从 $P_1$ 到 $P_2$ 的曲线之间的交叉角. 方位角被限制在区间 $0^{\circ }\le \delta <{360}^{\circ }$ 内.

评论 在导航中位置坐标通常以六十进度数给出; 球面距离, 航向角和方位角则以十进度数给出.

3.4.1.2 特殊坐标系

1. 地理坐标

为了确定地球表面的点 $P$ ,需要使用地理坐标(图 3.85),即具有地球半径的球面坐标: 地理经度 $\lambda$ 和地理纬度 $\phi$ .

为了确定经度度数, 人们将地球表面用从北极到南极的半大圆, 即所谓子午线进行划分. 零子午线通过格林尼治天文台. 由此出发人们借助 180 条子午线算出东经,同样借助180条子午线算出西经. 在赤道它们彼此相距 $111\mathrm{km}$ . 在给出东经时采用正值,西经则用负值给出. 因此 $-{180}^{\circ }\le \lambda \le {180}^{\circ }$ .

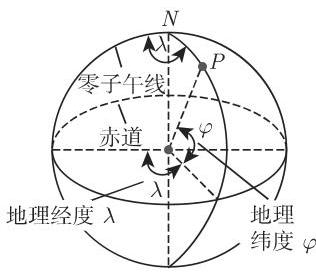
为了确定纬度, 人们将地球表面用平行于赤道的小圆进行划分. 从赤道开始向北算出 90 个纬度, 即北向纬度差, 同样算出 90 个南纬度. 北纬取正值, 南纬取负值. 因此 $-{90}^{\circ }\le \phi \le {90}^{\circ }$ .

2. 佐德纳坐标

在大范围测量中直角佐德纳 (Soldner) 坐标和高斯-克吕格坐标是重要的. 为了将弯曲的地球表面部分映射到平面中的直角坐标系, 在纵坐标方向保持距离, 按照佐德纳的做法,需要将 $x$ 轴放置在一条子午线 (称为中央子午线) 上,原点置于测量好的中央点 (图 3.86(a)). 点 $P$ 的纵坐标 $y$ 是 $P$ 和过 $P$ 点的球面正交曲线 (大圆) 在中央子午线上的垂足之间的弧段. 点 $P$ 的横坐标 $x$ 是 $P$ 和过中央点的主纬线之间的圆弧段, 其中该圆位于与中央子午线平行的一个平面内 (图 3.86(b)).

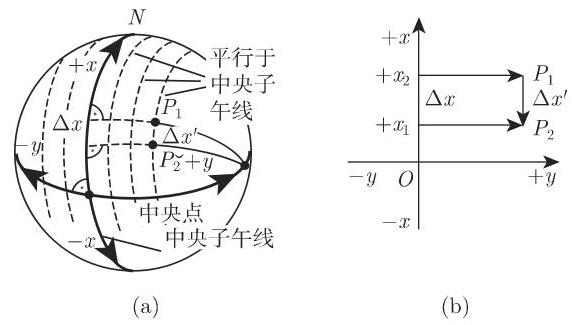
如果将球面横坐标和纵坐标转换成平面坐标系,那么线段 $\mathrm{\Delta }x$ 将被拉伸并且方向发生改变. 在横坐标方向上的伸长系数 $a$ 是

$$\begin{array}{}\text{(3.176)}& a=\frac{\mathrm{\Delta }x}{\mathrm{\Delta }{x}^{\prime }}=1+\frac{y^2}{2R^2},R=6371\mathrm{km}.\end{array}$$

为了调节拉伸,坐标系在中央子午线两侧的延伸不能超过 $64\mathrm{km}$ . 在 $y=$ $64\mathrm{km}$ 处 $1\mathrm{km}$ 长的线段具有 $0.05\mathrm{m}$ 的伸长量.

3. 高斯-克吕格坐标

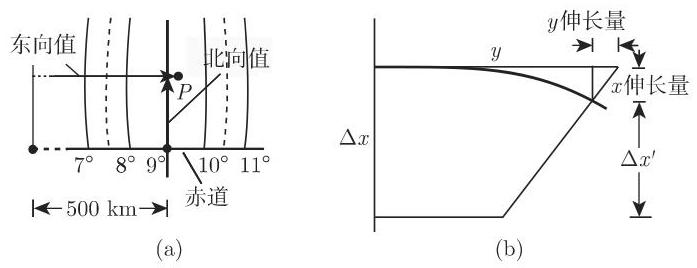
为了将弯曲的地球表面部分保角 (保形) 映射到平面上, 在高斯-克吕格坐标系中首先要划分出子午线带. 对德国来说这些中央子午线在东经 $6^{\circ },9^{\circ },{12}^{\circ }$ 和 ${15}^{\circ }$ (图 3.87(a)). 每个子午线带坐标系的原点位于中央子午线和赤道的交点处. 在南北方向要考虑全部范围,在东西方向则限制在两侧 $1^{\circ }{40}^{\prime }$ 宽的带内. 在德国它大约相当于 $\pm 100\mathrm{km}$ . 重叠部分是 ${20}^{\prime }$ ,这里近似于 $20\mathrm{km}$ .

横坐标方向上的伸长系数 (图 3.87(b)) 与在佐德纳坐标系 (3.176) 中一样. 为保持保角映射,需要将 $b$ 的量加到纵坐标:

$$\begin{array}{}\text{(3.177)}& b=\frac{y^3}{6R^2}.\end{array}$$

3.4.1.3 球面新月形或二角形

假设有两个平面 ${\mathrm{\Gamma }}_1$ 和 ${\mathrm{\Gamma }}_2$ 通过球的直径的端点 $A$ 和 $B$ 并围成一个角 $\alpha$ (图 3.88),由此确定两个大圆 $g_1$ 和 $g_2$ . 球面被两个大圆一半所界的部分称为球面新月形或球面二角形. 球面二角形的两边由大圆上 $A$ 和 $B$ 之间的球面距离定义, 两者都是 ${180}^{\circ }$ .

二角形的角定义为大圆 $g_1$ 和 $g_2$ 在点 $A$ 和 $B$ 处切线之间的夹角. 它们与平面 ${\mathrm{\Gamma }}_1$ 和 ${\mathrm{\Gamma }}_2$ 之间所谓的二面角 $\alpha$ 相同. 如果 $C$ 和 $D$ 是 $A$ 与 $B$ 之间两个大圆弧的平分点,则角 $\alpha$ 可以表示成 $C$ 与 $D$ 之间的球面距离. 球面二角形的面积 $A_b$ 随着 $\alpha$ 变到 ${360}^{\circ }$ 而与球的表面积成正比. 因此这个面积是

$$\begin{array}{}\text{(3.178)}& A_b=\frac{4\pi R^2\alpha }{{360}^{\circ }}=\frac{2R^2\alpha }{\varrho }=2R^2\mathrm{arc}\alpha ,\end{array}$$

这里 $\varrho$ 是如(3.175c)中的换算因子.

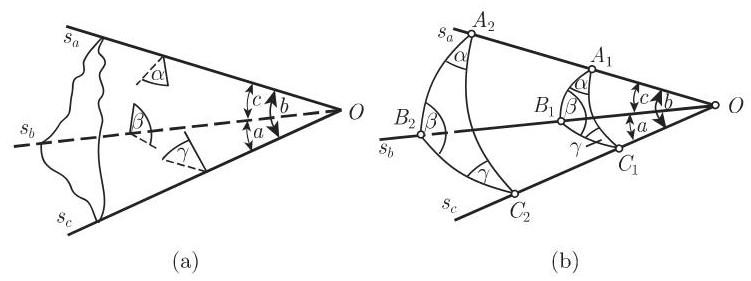
3.4.1.4 球面三角形

考虑球面上不在同一大圆上的三点 $A,B$ 和 $C$ . 将它们用大圆弧两两相连则得到一个球面三角形 $ABC$ (图 3.89).

该三角形的边定义为点之间的球面距离,即它们表示半径 $\overline{OA},\overline{OB}$ 和 $\overline{OC}$ 之间在球心处的夹角. 将它们记作 $a,b$ 和 $c$ ,并在以下用角的度量给出,而不管它们表示为球心处的夹角还是球面上的大圆弧. 球面三角形的三个角是三个大圆平面两两之间的夹角,记作 $\alpha ,\beta$ 和 $\gamma$ .

球面三角形的顶点, 边和角的记号顺序遵从与平面三角形一样的模式. 一个球面三角形如果至少有一个边等于 ${90}^{\circ }$ ,则称为直边三角形. 也存在着与平面直角三角形类似的球面直角三角形.

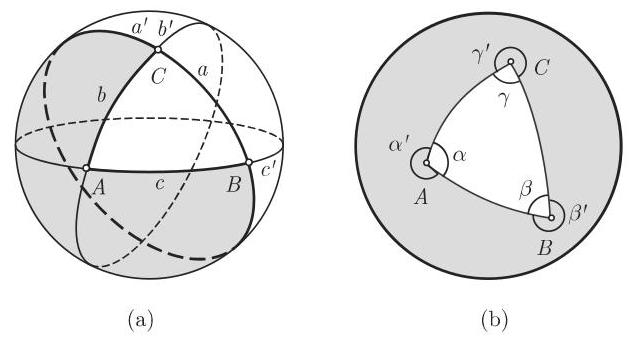
3.4.1.5 极三角形

1. 极点和极平面

球直径的端点 $P_1$ 和 $P_2$ 称为极点,与该直径垂直的大圆 $g$ 所在平面称为极平面(图 3.90). 极点与大圆 $g$ 上任一点之间的球面距离都是 ${90}^{\circ }$ . 极平面的方向是任意定义的: 沿选取方向横穿极平面, 左侧为左极点, 右侧为右极点.

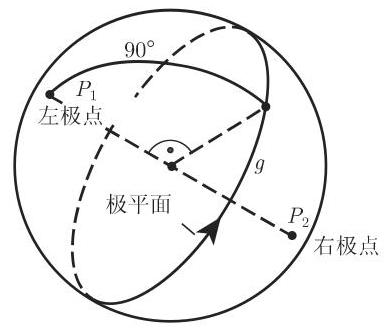
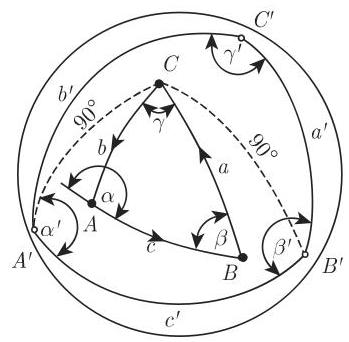
2. 极三角形

一个已知球面三角形 $ABC$ 的极三角形 $A^{\prime }{B}^{\prime }{C}^{\prime }$ 是这样一个球面三角形,使得对其边 (所在的大圆) 而言原来三角形的顶点是极点 (图 3.91). 对于每个球面三角形 $ABC$ 都存在一个极三角形 $A^{\prime }{B}^{\prime }{C}^{\prime }$ . 如果三角形 $A^{\prime }{B}^{\prime }{C}^{\prime }$ 是球面三角形 $ABC$ 的极三角形,那么三角形 $ABC$ 也是三角形 $A^{\prime }{B}^{\prime }{C}^{\prime }$ 的极三角形. 球面三角形的角与其极三角形相应的边是互补的角, 而球面三角形的边与其极三角形相应的角也是互补的角.

$$\begin{array}{}\text{(3.179a)}& a^{\prime }={180}^{\circ }-\alpha ,b^{\prime }={180}^{\circ }-\beta ,c^{\prime }={180}^{\circ }-\gamma ,\end{array}$$$$\begin{array}{}\text{(3.179b)}& {\alpha }^{\prime }={180}^{\circ }-a,{\beta }^{\prime }={180}^{\circ }-b,{\gamma }^{\prime }={180}^{\circ }-c.\end{array}$$

3.4.1.6 欧拉三角形与非欧拉三角形

一个球面三角形的顶点 $A,B,C$ 将每个大圆分成两个 (通常是不同的) 部分. 因此存在着若干具有相同顶点的不同三角形,例如,图 3.92(a) 中具有边 $a^{\prime },b,c$ 和阴影面的三角形. 根据欧拉定义,应该总是选取小于 ${180}^{\circ }$ 的弧作为球面三角形的边. 这对应于作为顶点之间球面距离的边的定义. 在这种情况下, 所有边和角都小于 ${180}^{\circ }$ 的球面三角形称为欧拉三角形,否则称为非欧拉三角形. 图 3.92(b) 中显示的是一个欧拉三角形和一个非欧拉三角形.

3.4.1.7 三面角

这是由从顶点 $O$ 出发的三条棱 $s_a,s_b,s_c$ 形成的三面立体 (图 3.93(a)). 角 $a$ , $b,c$ 定义为该三面角的边,它们中的每一个被两条棱所围. 两条棱之间的区域称为该三面角的面. 三面角的角 $\alpha ,\beta$ 和 $\gamma$ 是面之间的夹角. 如果三面角的顶点在球心 $O$ , 则它在球面上截出一个球面三角形 (图 3.93(b)). 该球面三角形以及相应的三面角的边和角是一致的, 因此对一个三面角得到的每个定理对于相应的球面三角形都成立, 反之亦然.