6.2.5 多元函数的极值

6.2.5.1 相对极值的定义

函数 $u=f\left(x_1,x_2,\cdots ,x_i,\cdots ,x_n\right)$ 称为在点 $P_0\left(x_{10},x_{20},\cdots ,x_{i0},\cdots ,x_{n0}\right)$ 具有相对极值,若存在数 $\epsilon$ ,满足对属于函数定义域区域 $x_{10}-\epsilon <x_1<x_{10}+\epsilon ,x_{20}-$ $\epsilon <x_2<x_{20}+\epsilon ,\cdots ,x_{n0}-\epsilon <x_n<x_{n0}+\epsilon$ 内的任意一点 $P\left(x_1,x_2,\cdots ,x_n\right)$ ,有不等式

$$\begin{array}{}\text{(6.68a)}& f\left(x_1,x_2,\cdots ,x_n\right)<f\left(x_{10},x_{20},\cdots ,x_{n0}\right)\end{array}$$

或

$$\begin{array}{}\text{(6.68b)}& f\left(x_1,x_2,\cdots ,x_n\right)>f\left(x_{10},x_{20},\cdots ,x_{n0}\right).\end{array}$$

利用多维空间的术语 (参见第 153 页 2.18.1), 若函数在一点比它邻域内的任何点都大或都小, 则称函数有相对极大值和相对极小值.

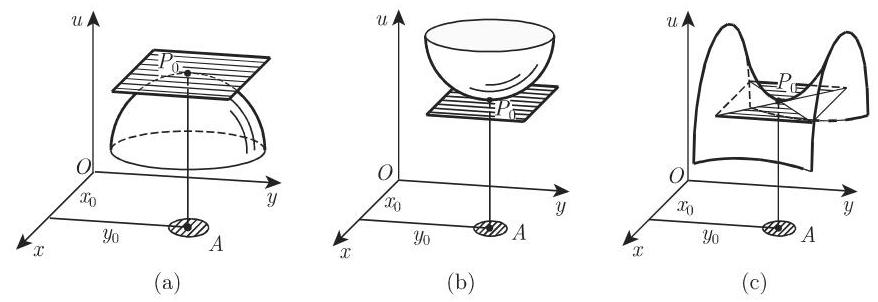
6.2.5.2 几何表示

二元函数在笛卡儿坐标系中表示一曲面 (参见第 154 页 2.18.1.2), 几何上其相对极值表示在点 $A$ ,曲面的竖坐标 (参见第 281 页 3.5.3.1,3.) 比在 $A$ 点的一个足够小的邻域内任何其他点的竖坐标都大或者都小 (图 6.16).

若曲面在定义域的内点 $P_0$ 处有极值,且在该点存在一个切平面,则该切平面平行于 $xOy$ 面 (图 6.16(a),(b)). 此性质是 $P_0$ 处取得极大值或极小值的必要非充分条件. 图 6.16(c) 则说明曲面在鞍点 $P_0$ 有水平切平面,但鞍点不是极值点.

6.2.5.3 二元可微函数极值的确定

若已知 $u=f\left(x,y\right)$ ,可解方程组 $f_x=0,f_y=0$ ,得点对 $\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots$ , 再将其代入二阶导数

$$\begin{array}{}\text{(6.69)}& A=\frac{{\partial }^{2}f}{\partial x^2},B=\frac{{\partial }^{2}f}{\partial x\partial y},C=\frac{{\partial }^{2}f}{\partial y^2}.\end{array}$$

利用表达式

$$\begin{array}{}\text{(6.70)}& \mathrm{\Delta }=\left|\begin{array}{ll}A& B\\ B& C\end{array}\right|=AC-B^2={[f_{xx}{f}_{yy}-{\left(f_{xy}\right)}^2]}_{x=x_i,y=y_i}\left(i=1,2,\cdots \right)\end{array}$$

可以判断是否存在极值以及极值类型:

(1) 当 $\mathrm{\Delta }>0$ 时,函数 $f\left(x,y\right)$ 在点 $\left(x_i,y_i\right)$ 有极值,且若 $f_{xx}<0,f\left(x,y\right)$ 有极大值,若 $f_{xx}>0,f\left(x,y\right)$ 有极小值 (充分条件).

(2) 当 $\mathrm{\Delta }<0$ 时,函数 $f\left(x,y\right)$ 无极值.

(3) 当 $\mathrm{\Delta }=0$ 时,需要进一步判断函数是否存在极值.

6.2.5.4 $n$ 元函数极值的确定

若已知 $u=f\left(x_1,x_2,\cdots ,x_n\right)$ ,首先可解由 $n$ 个方程构成的方程组

$$\begin{array}{}\text{(6.71)}& f_{x_1}=0,f_{x_2}=0,\cdots ,f_{x_n}=0,\end{array}$$

得 $\left(x_{10},x_{20},\cdots ,x_{n0}\right)$ ,这是由于 (6.71) 是函数有极值的必要非充分条件. 接下来建立一个由二阶偏导数构成的矩阵,满足 $a_{ij}=\frac{{\partial }^{2}f}{\partial x_i\partial x_j}$ . 然后将方程组 (6.71) 的解代入到 $a_{ij}$ 中,得到顺序主子式 (左上角的子式) $\left(a_{11},a_{11}{a}_{22}-a_{12}{a}_{21},\cdots \right)$ ,则存在如下情况:

(1) 若子式符号依次为 $-,+,-,+,\cdots$ ,则函数存在极大值.

(2) 若子式符号依次为 $+,+,+,+,\cdots$ ,则函数存在极小值.

(3) 若其中一些子式为 0 , 但非零子式的符号与上述两种情况相应位置的符号一致,则需要进一步判断函数是否有极值: 通常要检验 $\left(x_{10},x_{20},\cdots ,x_{n0}\right)$ 某一闭邻域内的函数值.

(4) 若子式符号不满足情形 1 和情形 2 中的符号规则, 则函数在该点无极值.

当然,二元函数是 $n$ 元函数情况的特例 (参见 [6.3]).

6.2.5.5 近似问题的解

借助多元函数极值的判定理论, 可以解决几类不同的近似问题, 如拟合问题和最小二乘问题.

用来解决的问题

• 确定傅里叶系数 (参见第 634 页 7.4.1.2, 1287 页 19.6.4.1).

• 确定可逼近函数的系数和参数 (参见第 1278 页 19.6.2).

• 确定超定线性方程组的近似解 (参见第 1246 页 19.2.1.3).

方法 解决上述问题的方法如下:

• 高斯最小二乘法 (例如参见第 1278 页 19.6.2).

• 最小二乘法 (参见第 1280 页 19.6.2.2).

• 均方 (连续或离散) 逼近 (参见第 1278 页 19.6.2).

• 观测 (或拟合)(参见第 1278 页 19.6.2) 与回归 (参见第 1097 页 16.3.4.2, 1.) 演算.

6.2.5.6 带有约束条件的极值问题

对于满足约束条件

$$\begin{array}{}\text{(6.72a)}& \phi \left(x_1,x_2,\cdots ,x_n\right)=0,\psi \left(x_1,x_2,\cdots ,x_n\right)=0,\cdots ,\chi \left(x_1,x_2,\cdots ,x_n\right)=0\end{array}$$

的 $n$ 元函数 $u=f\left(x_1,x_2,\cdots ,x_n\right)$ ,由于上述条件,变量不是相互独立的,若有 $k$ 个条件,显然必有 $k<n$ . 为了确定 $u$ 的极值,可能需要用条件方程组中的其他变量表示其中的 $k$ 个变量,并将其代入原函数,由此可转化为含 $n-k$ 个变量的无条件极值问题. 另一种方法是拉格朗日乘数法. 引入 $k$ 个未定乘数 $\lambda ,\mu ,\cdots ,\kappa$ ,得到含有 $n+k$ 个变量 $x_1,x_2,\cdots ,x_n,\lambda ,\mu ,\cdots ,\kappa$ 的拉格朗日函数

$$\mathrm{\Phi }\left(x_1,x_2,\cdots ,x_n,\lambda ,\mu ,\cdots ,\kappa \right)$$$$=f\left(x_1,x_2,\cdots ,x_n\right)+\lambda \phi \left(x_1,x_2,\cdots ,x_n\right)+\mu \psi \left(x_1,x_2,\cdots ,x_n\right)+\cdots$$$$\begin{array}{}\text{(6.72b)}& +\kappa \chi \left(x_1,x_2,\cdots ,x_n\right).\end{array}$$

函数 $\varphi$ 有极值的必要条件是关于变量 $x_1,x_2,\cdots ,x_n,\lambda ,\mu ,\cdots ,\kappa$ 的 $n+k$ 个方程构成的方程组 (6.71) 满足

$$\begin{array}{}\text{(6.72c)}& \phi =0,\psi =0,\cdots ,\chi =0,{\mathrm{\Phi }}_{x_1}=0,{\mathrm{\Phi }}_{x_2}=0,\cdots ,{\mathrm{\Phi }}_{x_n}=0.\end{array}$$

由于满足约束条件 (6.72a) 的函数 $f$ 在点 $P_0\left(x_{10},x_{20},\cdots ,x_{n0}\right)$ 取得极值的必要条件是 $x_{10},x_{20},\cdots ,x_{n0}$ 满足方程 (6.72c),因此可以在方程组 (6.72c) 的解 $x_{10}$ , $x_{20},\cdots ,x_{n0}$ 中寻找 $f$ 的极值点. 为了判断在满足该必要条件的点中是否真有极值点,还需要进一步的验证,其通用的方法相当复杂. 一般我们要据函数 $f$ 的特点采用一些恰当的、独特的计算方法来证明是否存在极值, 比如往往利用近似计算, 即对 $P_0$ 邻域内的函数值进行对比.

$◼$ 满足约束条件 $\phi \left(x,y\right)=0$ 的函数 $u=f\left(x,y\right)$ 的极值可以通过以下含有三个未知量的三个方程来确定:

$$\begin{array}{}\text{(6.73)}& \phi \left(x,y\right)=0,\frac{\partial }{\partial x}\left[f\left(x,y\right)+\lambda \phi \left(x,y\right)\right]=0,\frac{\partial }{\partial y}\left[f\left(x,y\right)+\lambda \phi \left(x,y\right)\right]=0.\end{array}$$

既然 (6.73) 中的三个方程仅为函数存在极值的必要非充分条件, 因此还需要进一步判断函数在这个方程组的解处是否取得极值, 其数学检验准则相当复杂 (参见 [6.3], [6.12]); 通常要比较函数在这些点的闭邻域内的取值.

(胡俊美 译)