Appearance
8.2.2 定积分的应用
8.2.2.1 定积分应用的一般原则
(1) 把要确定的量
(2) 把每个无穷小量
(3) 用一个变量
(4)要求的量为和式的极限:
其中对每个
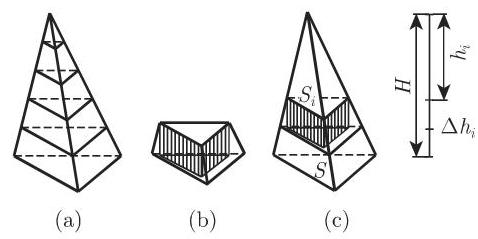
a) 将要求的体积
b) 用体积为
c) 把体积
d) 计算和的极限
8.2.2.2 在几何中应用
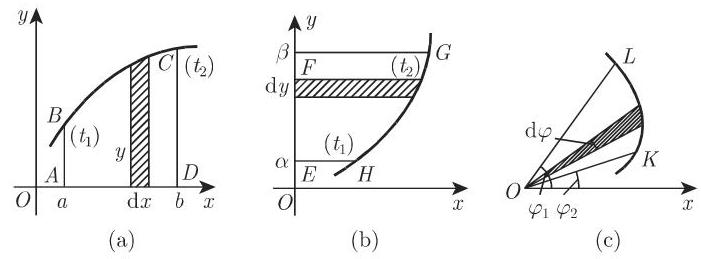
1. 平面图形的面积
(1)
(8.60a)
(2)
(3) 曲边扇形的面积 (图 8.12(c)) 曲边扇形以
要求更复杂图形的面积, 可将原图形化为一些简单图形, 或通过线积分 (参见第 684 页 8.3) 或二重积分 (参见第 694 页 8.4.1) 计算.
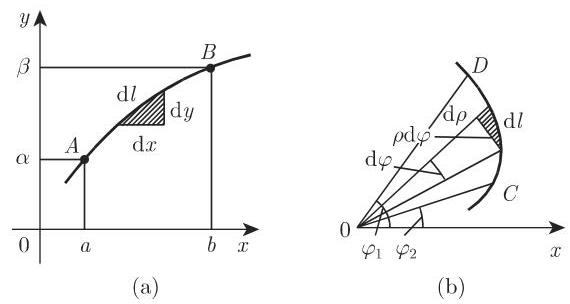
2. 平面曲线的弧长
(1) 由显形式
(8.61a)
由弧微分
- 利用 (8.61a) 计算椭圆的周长: 作代换
,有
其中
因为
(2) 由极坐标
由弧微分
3. 旋转体的表面积(也可参见第 673 页的第一古尔丁 (Guldin) 法则)
(1) 函数
(2) 函数
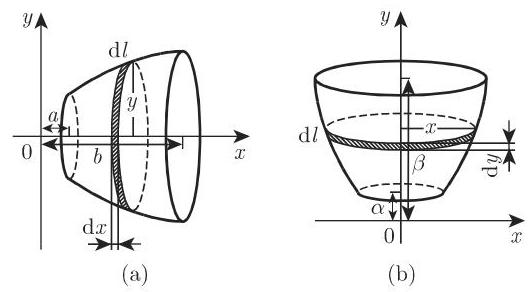
(3) 要计算更复杂的曲面面积, 可利用 699 页 8.4.1.3 中二重积分的应用以及 709 页 8.5.1.3 中的第一类曲面积分的应用. 700 页的表 8.9(二重积分的应用) 给出了利用二重积分求曲面面积的一般计算公式.
4. 体积 (也可参见第 673 页的第二古尔丁法则)
(1) 绕
(2) 绕
(3) 截面垂直于
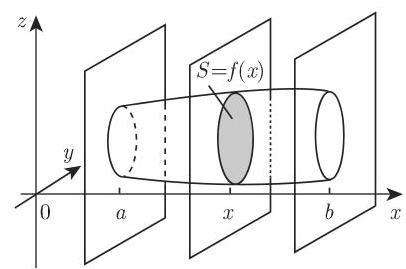
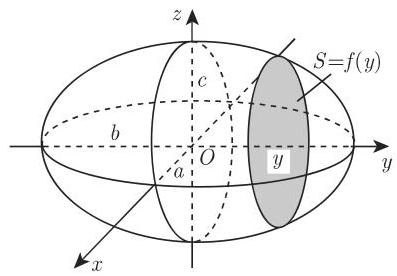
计算以原点为中心的旋转椭球体体积. 当
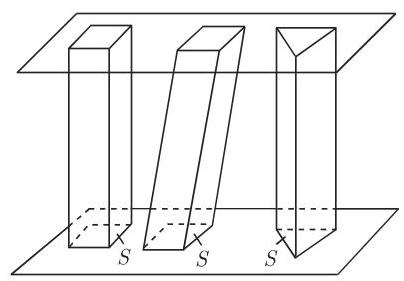
(4) 卡瓦列里 (Cavalieri) 原理 若在区间
最初的卡瓦列里原理是说: 夹在两个平行平面之间的两个立体图形, 被平行于这两个平面的任意平面所截, 如果所得的两个截面面积相等, 则这两个立体图形的体积相等 (图 8.17).
(5) 表 表 8.9(参见第 700 页二重积分的应用) 和表 8.10(参见第 705 页三重积分的应用) 给出了用多重积分来计算体积的一般公式.
8.2.2.3 在力学与物理中应用
1. 一点所走过的距离
设一动点的速度与时间有关,
2. 做功
力场中移动一物体时沿运动方向所做的功. 假设力场方向与运动方向恒定且都是沿
通常力场的方向与运动方向并不一致,此时功可以利用力与沿给定路径
3. 重力压力与侧压
在地球的重力场下,静止流体的密度为
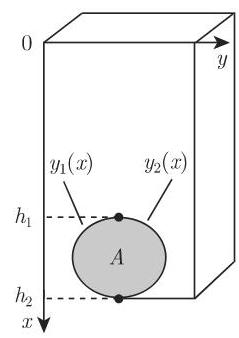
对于侧压
除以
函数
注 因为侧压与
4. 转动惯量
(1) 圆弧的转动惯量 区间
若密度是关于
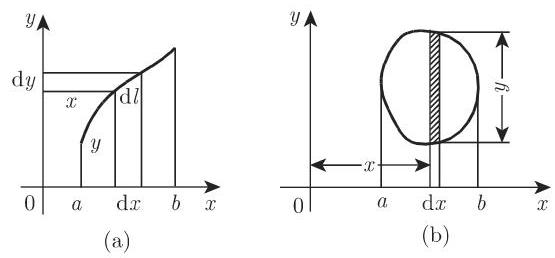
(2) 平面图形的转动惯量 质地均匀的密度为
其中
5. 重心与古尔丁法则
(1) 弧段的重心 考虑到 667 页的 (8.61a),区间
(2) 闭曲线的重心 长为
(3)第一古尔丁法则 设一平面曲线段绕同一平面内且不与之相交的轴旋转, 不妨取该轴为
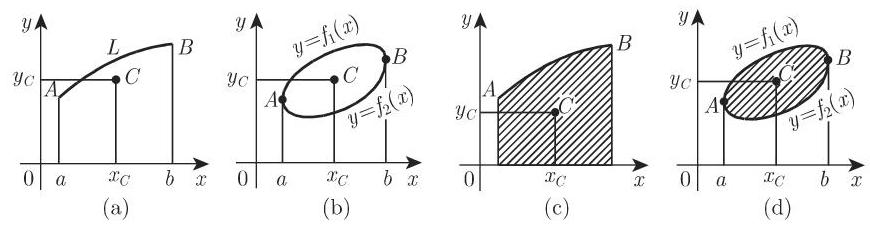
(4) 曲边梯形的重心 设
(5) 任意平面图形的重心 设有面积为
表 8.9 (700 页二重积分的应用) 和表 8.10(705 页三重积分的应用) 给出了利用多重积分来计算重心的公式.
(6) 第二古尔丁法则 假设一平面图形绕同一平面内且不与之相交的轴旋转, 不妨取该轴为