Appearance
17.2.3 李雅普诺夫指数
1. 矩阵的奇异值
设
奇异值有几何上的解释: 如果
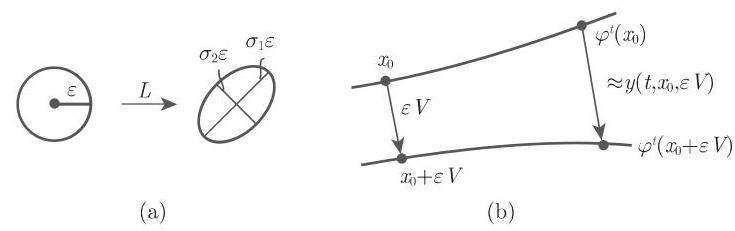
2. 李雅普诺夫指数的定义
设
满足
3. 李雅普诺夫指数的计算
若将位于
设
在离散情形 (17.3) 下, 所有李雅普诺夫指数之和为
因此对耗散系统,
4. 测度熵与李雅普诺夫指数
设
等式
一般不成立 (可参见第 1153 页 17.2.4.4,
Appearance
设
奇异值有几何上的解释: 如果

设
满足
若将位于
设
在离散情形 (17.3) 下, 所有李雅普诺夫指数之和为
因此对耗散系统,
设
等式
一般不成立 (可参见第 1153 页 17.2.4.4,