5.1.1 命题演算

1. 命题

命题是一个事实的思想反映, 它表示为自然或人工语言下的一个句子. 每个命题被考虑为是真的或是假的. 这是二值性原理 (与多值性及模糊逻辑不同, 参见第 554 页 5.9.1). “真”和“假”被称为命题的真值, 并且将它们分别记为 T(或 1) 和 $\mathrm{F}\left(\text{或 }0\right)$ . 真值可以看作命题常数.

2. 命题联结词

命题逻辑研究命题的复合的真值, 它们取决于分量的真值, 只是与命题对应的语句的外延被考虑. 因此复合的真值仅与分量的真值及所使用的运算有关. 于是, 特别地, 命题运算

“非 $A$ ” $\left(\mathrm{\neg }A\right)$ ,(5.1)

“ $A$ 和 $B$ ” $\left(A\wedge B\right)$ ,(5.2)

“ $A$ 或 $B$ ” $\left(A\vee B\right)$ ,(5.3)

“若 $A$ ,则 $B$ ” $\left(A\Rightarrow B\right)$ ,(5.4)

以及

$$\begin{array}{}\text{(5.5)}& \text{“}A\text{当且仅当}B\text{”}\left(A\iff B\right)\end{array}$$

的结果的真值由分量的真值确定. 这里“逻辑或”总意味“包括或”, 也就是“和/或”. 在蕴涵情形,对于 $A\Rightarrow B$ ,也使用下列词语表达的形式:

$A$ 蕴涵 $B,B$ 对于 $A$ 是必须的, $A$ 对于 $B$ 是充分的.

3. 真值表

在命题演算中,命题 $A$ 和 $B$ 被看作变量 (命题变量),它们可以只取值 $\mathrm{F}$ 和 $\mathrm{T}$ . 于是表 5.1 中的真值表含有定义命题运算的真值函数.

4. 命题演算中的公式

命题演算中的复合表达式 (公式)可以由命题变量通过一元运算 (否定) 和二元运算 (合取、析取、蕴涵和等价) 合成. 这些表达式即公式是用归纳的方式定义的:

表 5.1 命题演算的真值表

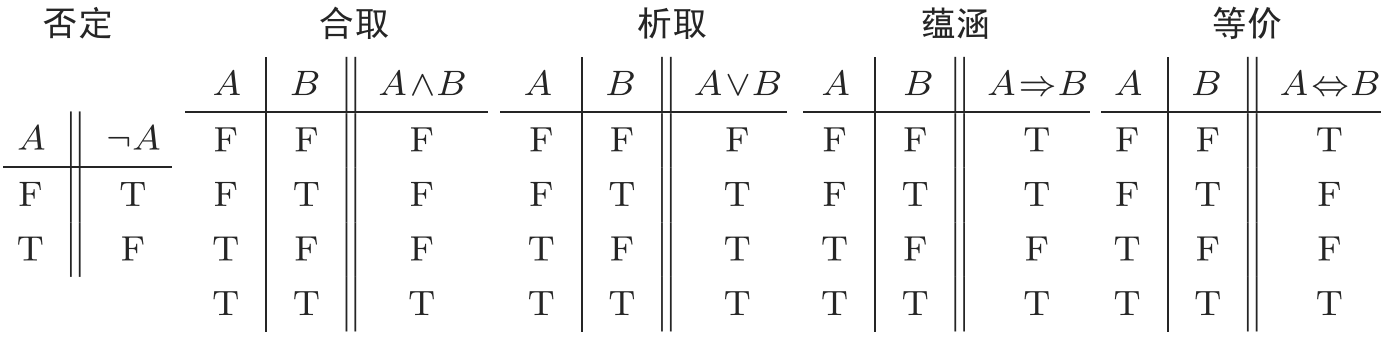
(1) 命题变量及常数 $\mathrm{T},\mathrm{F}$ 是公式.(5.6)

(2) 如果 $A$ 和 $B$ 是公式,那么 $\left(\mathrm{\neg }A\right),\left(A\wedge B\right),\left(A\vee B\right),\left(A\Rightarrow B\right),\left(A\iff B\right)$ 也是公式.(5.7)

为简化公式, 在引进优先规则后圆括号可以省略. 在下列序列中每个命题运算都比序列中下一个运算约束得更强:

$$\mathrm{\neg },\wedge ,\vee ,\Rightarrow ,\iff \text{.}$$

记号 $\overline{A}$ 常用来代替“ $\mathrm{\neg }A$ ”,并且省略符号 $\wedge$ . 借助这些简化,例如,公式 $(\left(A\vee \left(\mathrm{\neg }B\right)\right)\Rightarrow$ $\left(\left(A\wedge B\right)\vee C\right))$ 可以改写为更简明的形式:

$$A\vee \overline{B}\Rightarrow A\overline{B}\vee C.$$

5. 真值函数

对公式的每个命题变量指定一个真值, 这种指派称为命题变量的解释. 应用命题运算的定义 (真值表) 对于变量的每个可能的解释我们可以对公式指定真值. 例如, 上面的公式确定三个变量的真值函数 (布尔函数参见第 530 页 5.7.5).

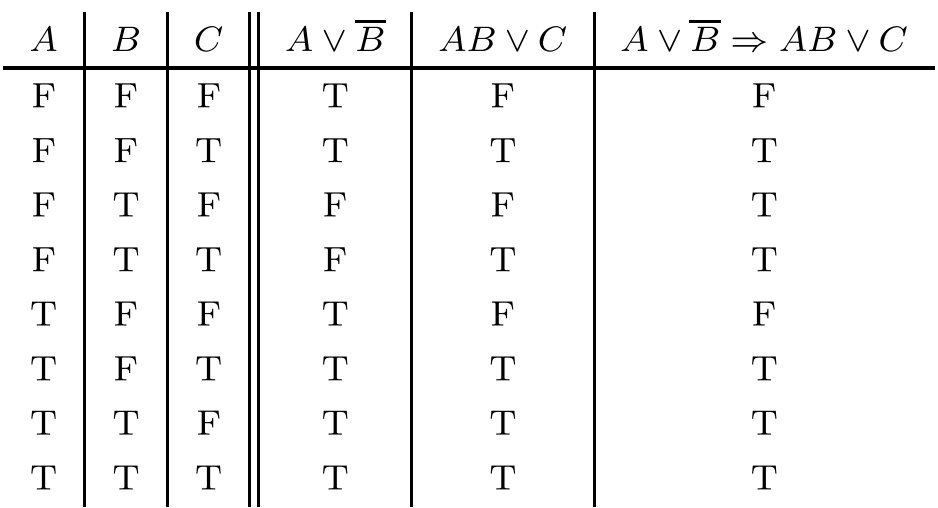
因此,每个有 $n$ 个命题变量的公式确定一个 $n$ 位 (或 $n$ 项) 真值函数,即对每个 $n$ 真值组指派一个真值的函数. 存在 $2^{2^n}$ 个 $n$ 位真值函数,特别地,这些是 16 个二元函数.

6. 命题演算的基本定律

若两个命题公式 $A$ 和 $B$ 确定相同的真值函数,则称它们逻辑等价或语义等价, 并记为 $A=B$ . 因此命题公式的逻辑等价性可以通过真值表检验. 例如,由上面给出的公式的真值表可知,有 $A\vee \overline{B}\Rightarrow AB\vee C=B\vee C$ ,即公式 $A\vee \overline{B}\Rightarrow AB\vee C$ 实际上与 $A$ 无关. 特别地,有下列命题演算的基本定律:

(1) 结合律

$$\begin{array}{}\text{(5.8a)}& \left(A\wedge B\right)\wedge C=A\wedge \left(B\wedge C\right),\end{array}$$$$\begin{array}{}\text{(5.8b)}& \left(A\vee B\right)\vee C=A\vee \left(B\vee C\right).\end{array}$$

(2) 交换律

$$\begin{array}{}\text{(5.9a)}& A\wedge B=B\wedge A,\end{array}$$$$\begin{array}{}\text{(5.9b)}& A\vee B=B\vee A.\end{array}$$

(3) 分配律

$$\begin{array}{}\text{(5.10a)}& \left(A\vee B\right)C=AC\vee BC,\end{array}$$$$\begin{array}{}\text{(5.10b)}& AB\vee C=\left(A\vee C\right)\left(B\vee C\right).\end{array}$$

(4) 吸收律

$$\begin{array}{}\text{(5.11a)}& A\left(A\vee B\right)=A,\end{array}$$$$\begin{array}{}\text{(5.11b)}& A\vee AB=A.\end{array}$$

(5) 幂等性律

$$\begin{array}{}\text{(5.12a)}& AA=A,\end{array}$$$$\begin{array}{}\text{(5.12b)}& A\vee A=A\text{.}\end{array}$$

(6) 排中律

$$\begin{array}{}\text{(5.13a)}& A\overline{A}=\mathrm{F},\end{array}$$$$\begin{array}{}\text{(5.13b)}& A\vee \overline{A}=\mathrm{T}.\end{array}$$

(7) 德摩根法则

$$\begin{array}{}\text{(5.14a)}& \overline{AB}=\overline{A}\vee \overline{B}\end{array}$$$$\begin{array}{}\text{(5.14b)}& \overline{A\vee B}=\overline{A}\overline{B}.\end{array}$$

(8) 对于 $\mathrm{T}$ 和 $\mathrm{F}$ 的定律

$$\begin{array}{}\text{(5.15a)}& A\mathrm{T}=A,\end{array}$$$$\begin{array}{}\text{(5.15b)}& A\vee \mathrm{F}=A,\end{array}$$$$\begin{array}{}\text{(5.15c)}& A\mathrm{F}=\mathrm{F},\end{array}$$$$\begin{array}{}\text{(5.15d)}& A\vee \mathrm{T}=\mathrm{T}\end{array}$$$$\begin{array}{}\text{(5.15e)}& \bar{\mathrm{T}}=\mathrm{F},\end{array}$$$$\begin{array}{}\text{(5.15f)}& \bar{\mathrm{F}}=\mathrm{T}\text{.}\end{array}$$

(9) 双重否定

$$\begin{array}{}\text{(5.16)}& \bar{\overline{A}}=A\text{.}\end{array}$$

应用对于蕴涵和等价的真值表可得到恒等式

$$\begin{array}{}\text{(5.17a)}& A\Rightarrow B=\overline{A}\vee B,\end{array}$$$$\begin{array}{}\text{(5.17b)}& A\iff B=AB\vee \overline{A}\overline{B}.\end{array}$$

因此蕴涵和等价可以通过其他命题运算表示. 定律 (5.17a), (5.17b) 被用于改述命题公式.

恒等式 $A\vee \overline{B}\Rightarrow AB\vee C=B\vee C$ 可以验证如下: $A\vee \overline{B}\Rightarrow AB\vee C=$ $\overline{A\vee \overline{B}}\vee AB\vee C=\overline{A}\bar{\overline{B}}\vee AB\vee C=\overline{A}B\vee AB\vee C=\left(\overline{A}\vee A\right)B\vee C=TB\vee C=B\vee C$ .

(10) 其他变换

$$\begin{array}{}\text{(5.18a)}& A\left(\overline{A}\vee B\right)=AB,\end{array}$$$$\begin{array}{}\text{(5.18b)}& A\vee \overline{A}B=A\vee B,\end{array}$$$$\begin{array}{}\text{(5.18c)}& \left(A\vee C\right)\left(B\vee \overline{C}\right)\left(A\vee B\right)=\left(A\vee C\right)\left(B\vee \overline{C}\right),\end{array}$$$$\begin{array}{}\text{(5.18d)}& AC\vee B\overline{C}\vee AB=AC\vee B\overline{C}.\end{array}$$

(11) NAND 函数和 NOR 函数 众所周知, 每个命题公式确定一个真值函数. 检验这个语句的如下的逆: 每个真值函数可以表示为命题逻辑中一个适当公式的真值表. 依据 (5.17a) 和 (5.17b), 蕴涵和等价可以从公式中消去 (还可见第 528 页 5.7). 这个事实及德摩根 (De Morgan) 法则 (5.14a) 和 (5.14b) 蕴涵着我们可以仅通过否定和析取或者否定和合取表示每个公式, 因而表示每个真值函数. 还存在另外两个二变量的二元真值函数适宜用于表示所有真值函数. 它们称为 NAND 函数或谢费尔 (Sheffer) 函数 (记号是 “|”) 以及 NOR 函数或皮尔斯 (Peirce) 函数 (记号是 “ $\downarrow$ ”),并且在表 5.2 和表 5.3 中给出它们的真值表. 将这些运算的真值表与合取和析取的真值表加以比较就可明白术语 NAND 函数 (NOT AND) 及 NOR 函数 (NOT OR) 的意义.

$A$	$B$	$A\mid B$
F	F	T
F	T	T
T	F	T
T	T	F

	$A$	$B$	$A\downarrow B$
	F	F	T
	F	T	F
	T	F	F
	T	T	F

7. 重言式、数学中的推理

如果命题演算中一个公式的真值函数的值恒为 $\mathrm{T}$ ,那么将它称为重言式. 因此, 如果公式 $A\iff B$ 是重言式,那么称两个公式 $A$ 和 $B$ 逻辑等价. 命题演算定律经常表现数学中使用的推理方法. 作为一个例子, 我们考虑换位律, 即重言式

$$\begin{array}{}\text{(5.19a)}& A\Rightarrow B\iff \overline{B}\Rightarrow \overline{A}.\end{array}$$

这个定律还有形式

$$\begin{array}{}\text{(5.19b)}& A\Rightarrow B=\overline{B}\Rightarrow \overline{A}\text{.}\end{array}$$

可以这样解释这个定律: 证明 $B$ 是 $A$ 的推论与证明 $\overline{A}$ 是 $\overline{B}$ 的推论是一回事. 问接证明(还可参见第 6 页 1.1.2.2) 是基于下列原理: 为了证明 $B$ 是 $A$ 的推论,我们假设 $B$ 错误,并且在 $A$ 正确的假设下导出矛盾. 在命题演算中可以用多种方式将这个原理形式化:

$$\begin{array}{}\text{(5.20a)}& A\Rightarrow B=A\overline{B}\Rightarrow \overline{A}\end{array}$$

或

$$\begin{array}{}\text{(5.20b)}& A\Rightarrow B=A\overline{B}\Rightarrow B\end{array}$$

或

$$\begin{array}{}\text{(5.20c)}& A\Rightarrow B=A\overline{B}\Rightarrow \mathrm{F}\end{array}$$