Appearance
8.1.1 原函数或反导数
1. 定义
设
则
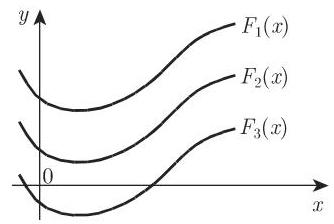
2. 练习
区间
8.1.1.1 不定积分
函数
积分号
8.1.1.2 初等函数的积分
1. 基本积分
以解析形式表示的初等函数的积分可化为一系列基本积分, 而因为不定积分即为确定函数
表 8.1 中的积分公式源自 583 页表 6.1 中微分公式 (初等函数的导数) 的逆运算,略去了积分常数
幂函数 | 指数函数 |
三角函数 | 双曲函数 |
分式有理函数 | 无理函数 |
2. 一般积分
为了解决积分问题, 应尽量利用代数变换、三角变换以及基本积分的积分法则将给定积分化简. 在很多情况下, 具有初等原函数的函数都能通过 8.1.2 中的积分方法加以积分. 1382 页中的表 21.7(不定积分) 列出了某些积分结果. 在积分中下面的注有着重要作用:
a) 通常可以忽略积分常数, 除非某些积分在不同形式时可用不同的任意常数来表示;
b) 若原函数中存在一个含
c) 若原函数以幂级数的形式给出, 则函数不能按初等方法积分.
[8.1] 和 [8.3] 中给出了更多的积分形式及结果.