Appearance
17.3.1 莫尔斯-斯梅尔系统中的分岔
令
局部分岔和全局分岔的区别在于: 局部分岔发生在系统单个轨道的邻域附近, 而全局分岔影响相空间的大部分区域.
17.3.1.1 定常状态邻域中的局部分岔
1. 中心流形
考虑含参数微分方程
其中
进一步,假设当
进一步,假定
由微分方程的中心流形定理(Shoshitaishvili 定理, 见 [17.14]) 可知, 对于在 0 的邻域中的
其中
由表达式 (17.68) 可知, 在 0 的邻域中的 (17.67) 的分岔可由微分方程
唯一描述. 方程 (17.69) 代表约化到 (17.68) 的局部中心流形
2. 鞍结点分岔和跨临界分岔
取 (17.67) 中的
可微函数
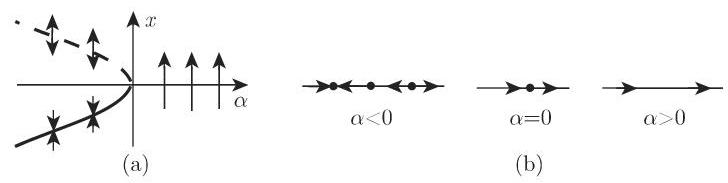
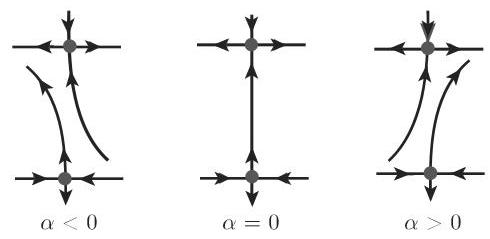
多维情形导致了 (17.67) 在 0 的邻域中的鞍结点分岔. 当
若在这些关于
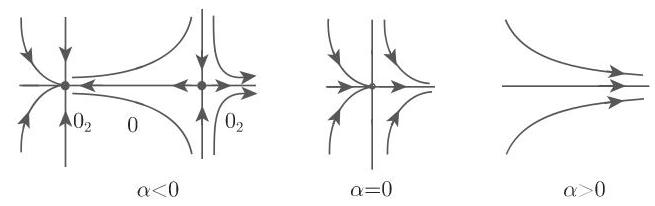
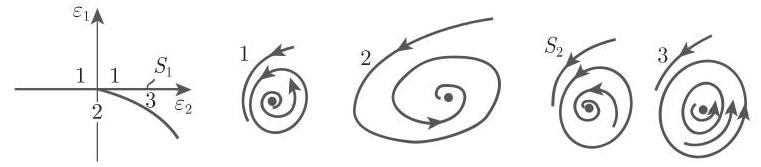
3. 霍普夫分歧
取 (17.67) 中的
其中
其中省略号表示高阶项. 由 (17.72) 的系数函数的泰勒展开可得到截尾正规形式
安德罗诺夫 (Andronov)-霍普夫定理确保了当
在条件
(1)
**a)
**b)
**c)
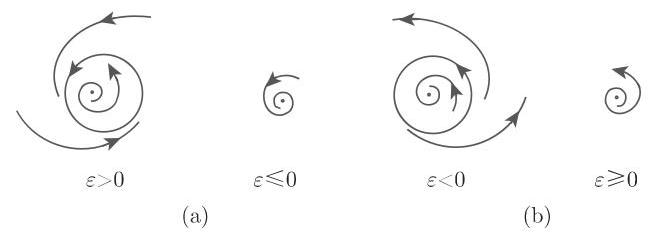
(2)
**a)
**b)
**c)
对于初始系统 (17.67), 上述情形的阐释展示了一个复合平衡点 (重数为 1 的复合焦点) 的极限环的分岔, 它被称为 霍普夫分歧(或者安德罗诺夫-霍普夫分歧). 当
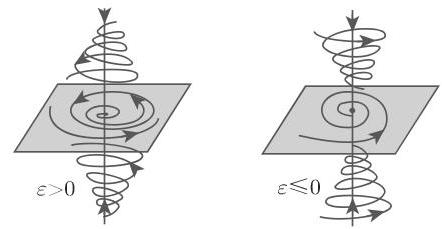
霍普夫分歧是通有的, 且有余维数为 1 . 以上情形表明在上述假设下, 超临界霍普夫分歧可由焦点的稳定性识别: 假设在 0 处的 (17.67) 右边的雅可比矩阵的特征值满足
含参数
当
(17.75) 在平衡点(0,0)处的雅可比矩阵的特征值为
正如第 1125 页 17.1.2.3,1. 中的例子,(0,0)点是(17.75)在
4. 双参数微分方程中的分岔
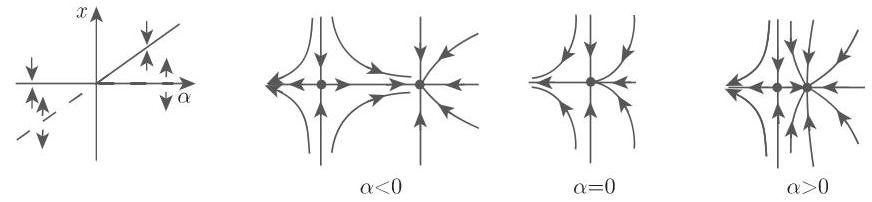
(1) 尖点分岔 取定 (17.67) 中
集合
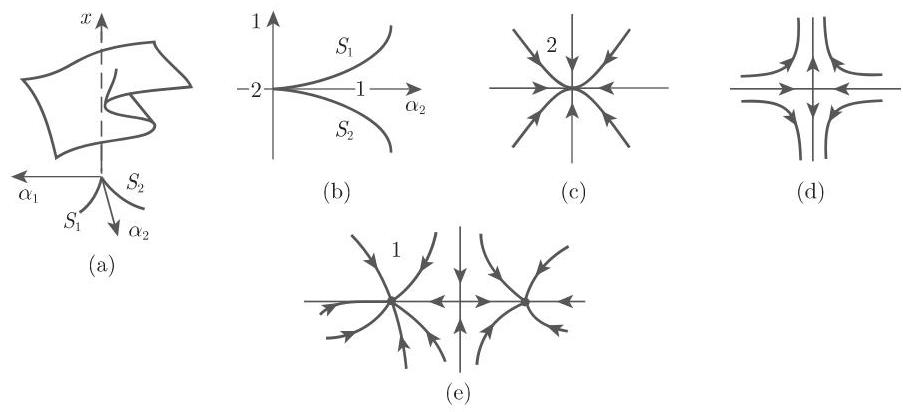
接下来,假定
从点
(17.67) 的二维相空间情形的相图如图 17.26(c),(e) 所示. 当
(2) 波格丹诺夫-塔肯 (Bogdanov-Takens) 分岔 取 (17.67) 中的
于是在曲线
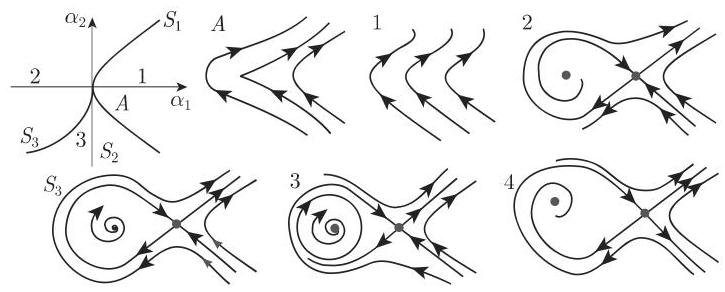
这种分岔具有全局属性, 我们称之为由鞍点的同宿轨产生单一周期轨道, 或者称之为分界线环消失.
(3) 广义霍普夫分歧 假定在 (17.67) 中,对于
5. 对称破缺
某些微分方程 (17.67) 在下列意义下有对称性: 存在线性变换
我们讨论在
取
17.3.1.2 在周期轨邻域中的局部分岔
1. 映射的中心流形定理
当
于是对于开集
且在
由 (17.79) 可知,(17.78)在(0,0)附近的分岔由下列定义在局部中心流形
唯一描述.
2. 二重半稳定周期轨的分岔
在系统 (17.67) 中取定
或者
在 0 附近对 (17.81a) 作迭代,对应于不同的
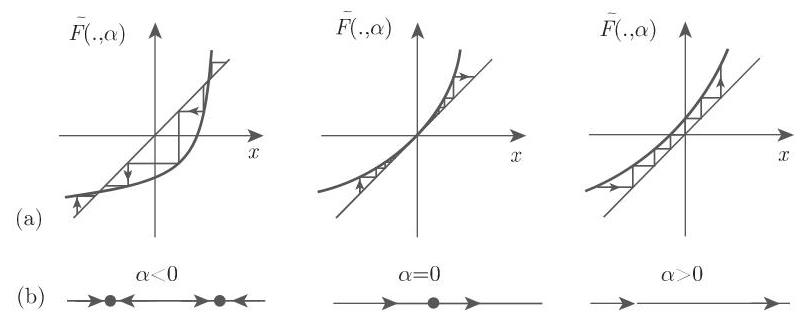
在微分方程 (17.67) 的情形下, 映射 (17.81a) 的性质描述了一个二重半稳定周期轨的分岔: 当
3. 周期加倍或 Flip 分岔
在系统(17.67)中取定
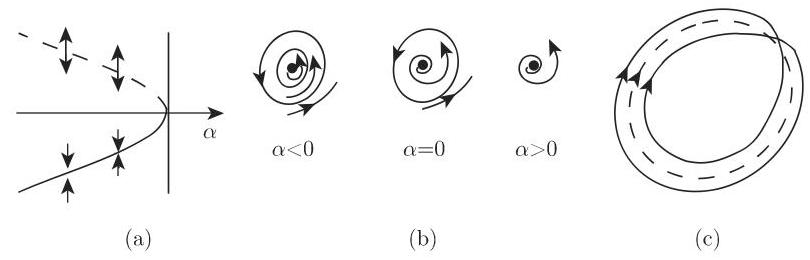
则在 0 附近庞加莱映射的分岔行为可由满足条件
当
一般地,对于
(17.83)
则在
对于微分方程 (17.67),由映射 (17.82) 的性质可推出在
定义逻辑斯谛映射
给出.
映射具有下列分岔行为 (见 [17.9]): 当
当
当
逻辑斯谛映射的分岔行为也能在一类单峰映射中找到. 即, 具有单个极大值的区间
4. 环面的产生
考虑系统 (17.67),取定
由中心流形定理可知,此时存在一个
对于较小的
若对于较小的
这里
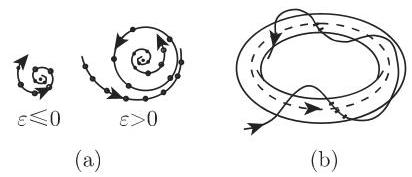
Neimark-Sacker 定理 (见 [17.18],[17.3]) 表明 (17.86) 的分岔行为与
在映射 (17.85) 中, 取定
在
关于微分方程 (17.67),映射 (17.85) 的闭不变曲线的存在意味着当
17.3.1.3 全局分岔
除了当分界线环消失时所出现的周期生成轨, (17.67) 可以有另外的全局分岔. 其中的两个作为例子在 [17.11] 中说明.
1. 源自鞍结点消失的周期轨的出现
含参数系统
在极坐标
显然,对于任意参数

2. 平面上鞍-鞍形分界线环的消失
考虑含参数平面微分方程
当