5.2.2 集合运算

1. 维恩图

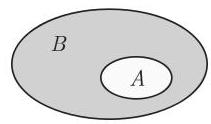
若用平面图形表示集合, 以此给出集合及集合运算的图形解释, 就是所谓 维恩 (Venn) 图解. 例如,图 5.1 表示子集关系 $A\subseteq B$ .

2. 并、交、补

借助集合运算, 可以用不同方式由给定集合形成新的集合:

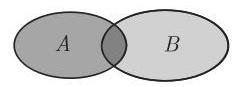
(1) 并 设 $A$ 和 $B$ 是两个集合. 它们的并集或并(记作 $A\cup B$ ) 定义为

$$\begin{array}{}\text{(5.39)}& A\cup B=\{x\mid x\in A\vee x\in B\},\end{array}$$

读作 “ $A$ 并 $B$ ” 或 “ $A$ 与 $B$ 的并”. 如果 $A$ 和 $B$ 分别由性质 $E_1$ 和 $E_2$ 给定,那么并集 $A\cup B$ 具有至少其中一个性质,即至少属于其中一个集合的元素. 图 5.2 中阴影区域表示并集.

$\{1,2,3\}\cup \{2,3,5,6\}=\{1,2,3,5,6\}.$

(2) 交 设 $A$ 和 $B$ 是两个集合. 它们的交集或交、割、割集 (记作 $A\cap B$ ) 定义为

$$\begin{array}{}\text{(5.40)}& A\cap B=\{x\mid x\in A\wedge x\in B\},\end{array}$$

读作 “ $A$ 与 $B$ 的交” 或 “ $A$ 交 $B$ ”. 如果 $A$ 和 $B$ 分别由性质 $E_1$ 和 $E_2$ 给定,那么交集 $A\cup B$ 具有性质 $E_1$ 和 $E_2$ ,即同时属于这两个集合的元素. 图 5.3 中阴影区域表示交集.

我们可以用两个数 $a$ 和 $b$ 的因子集合 $T\left(a\right)$ 和 $T\left(b\right)$ 的交来定义最大公因子 (参见第 499 页 5.4.1.4). 对于 $a=12$ 和 $b=18$ ,有 $T\left(a\right)=\{1,2,3,4,6,12\}$ 和 $T\left(b\right)=\{1,2,3,6,9,18\}$ ,所以 $T\left(12\right)\cap T\left(18\right)$ 含有公因子,并且最大公因子是 $gcd\left(12,18\right)=6$ .

(3) 不相交集 若两个集合 $A$ 和 $B$ 没有公共元素,则称它们是不相交的. 对于它们, 有

$$\begin{array}{}\text{(5.41)}& A\cap B=\varnothing ,\end{array}$$

即它们的交是空集.

奇数集和偶数集不相交; 它们的交是空集, 即

$$\{\text{奇数}\}\cap \{\text{偶数}\}=\varnothing \text{.}$$

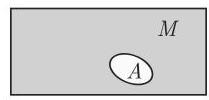
(4) 补 如果只考虑一个给定集合 $M$ 的子集,那么 $A$ 对于 $M$ 的补集或补 $C_M\left(A\right)$ 含有 $M$ 的所有不属于 $A$ 的元素:

$$\begin{array}{}\text{(5.42)}& C_M\left(A\right)=\{x\mid x\in M\vee x\notin A\},\end{array}$$

读作 “ $A$ 对于 $M$ 的补”,并且 $M$ 称为基本集,有时也称为泛集. 如果基本集 $M$ 显然来自所考虑的问题,那么也用记号 $\overline{A}$ 表示补集. 图 5.4 中阴影区域表示补集.

3. 集代数的基本律

集合运算具有与逻辑运算类似的性质. 集代数的基本律是 (1) 结合律

$$\begin{array}{}\text{(5.43)}& \left(A\cap B\right)\cap C=A\cap \left(B\cap C\right),\end{array}$$$$\begin{array}{}\text{(5.44)}& \left(A\cup B\right)\cup C=A\cup \left(B\cup C\right).\end{array}$$

(2) 交换律

$$\begin{array}{}\text{(5.45)}& A\cap B=B\cap A,\end{array}$$$$\begin{array}{}\text{(5.46)}& A\cup B=B\cup A.\end{array}$$

(3) 分配律

$$\begin{array}{}\text{(5.47)}& \left(A\cup B\right)\cap C=\left(A\cap C\right)\cup \left(B\cap C\right),\end{array}$$$$\begin{array}{}\text{(5.48)}& \left(A\cap B\right)\cup C=\left(A\cup C\right)\cap \left(B\cup C\right).\end{array}$$

(4) 吸收律

$$\begin{array}{}\text{(5.49)}& A\cap \left(A\cup B\right)=A,\end{array}$$$$\begin{array}{}\text{(5.50)}& A\cup \left(A\cap B\right)=A\text{.}\end{array}$$

(5) 幂等律

$$\begin{array}{}\text{(5.51)}& A\cap A=A,\end{array}$$$$\begin{array}{}\text{(5.52)}& A\cup A=A.\end{array}$$

(6) 德摩根律

$$\begin{array}{}\text{(5.53)}& \overline{A\cap B}=\overline{A}\cup \overline{B}\end{array}$$$$\begin{array}{}\text{(5.54)}& \overline{A\cup B}=\overline{A}\cap \overline{B}.\end{array}$$

(7) 一些其他定律

$$\begin{array}{}\text{(5.55)}& A\cap \overline{A}=\varnothing ,\end{array}$$$$\begin{array}{}\text{(5.56)}& A\cup \overline{A}=M\left(M\text{是基本集}\right),\end{array}$$$$\begin{array}{}\text{(5.57)}& A\cap M=A,\end{array}$$$$\begin{array}{}\text{(5.58)}& A\cup \varnothing =A,\end{array}$$$$\begin{array}{}\text{(5.59)}& A\cap \varnothing =\varnothing ,\end{array}$$$$\begin{array}{}\text{(5.60)}& A\cup M=M,\end{array}$$$$\begin{array}{}\text{(5.61)}& \overline{M}=\varnothing \end{array}$$$$\begin{array}{}\text{(5.62)}& \overline{\varnothing }=M\end{array}$$$$\begin{array}{}\text{(5.63)}& \bar{\overline{A}}=A\text{.}\end{array}$$

这个表也可以应用下列代换从命题演算基本律 (参见第 434 页 5.1.1) 得到: $\cap$ 代 $\wedge ,\cup$ 代 $\vee ,M$ 代 $\mathrm{T}$ ,以及 $\varnothing$ 代 $\mathrm{F}$ . 这个一致性不是偶然的; 我们将在 528 页 5.7 讨论它.

4. 其他的集运算

除了上面定义的运算外,这里定义两个集合 $A$ 和 $B$ 间的一些其他运算: 差集或差 $A\setminus B$ ,对称差 $A△B$ ,以及笛卡儿积 $A\times B$ .

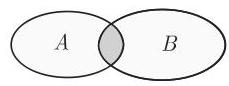
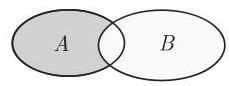
(1) 两个集合的差 $A$ 的不属于 $B$ 的元素的集合称作 $A$ 与 $B$ 的差集 或差:

$$\begin{array}{}\text{(5.64a)}& A\setminus B=\{x\mid x\in A\wedge x\notin B\}.\end{array}$$

如果 $A$ 由性质 $E_1,B$ 由性质 $E_2$ 定义,那么 $A\setminus B$ 含有具有性质 $E_1$ 但不具有性质 $E_2$ 的元素.

图 5.5 中阴影区域表示差集.

$\{1,2,3,4\}\setminus \{3,4,5\}=\{1,2\}.$

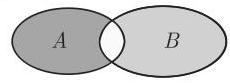
(2) 两个集合的对称差 对称差 $A△B$ 是所有恰好属于集合 $A$ 和 $B$ 之一的元素的集合:

$$\begin{array}{}\text{(5.64b)}& A△B=\{x\mid \left(x\in A\vee x\notin B\right)\wedge \left(x\in B\vee x\notin A\right)\}.\end{array}$$

由定义可知

$$\begin{array}{}\text{(5.64c)}& A△B=\left(A\setminus B\right)\cup \left(B\setminus A\right)=\left(A\cup B\right)\setminus \left(A\cap B\right),\end{array}$$

即对称差含有恰好具有定义性质 $E_1$ (对于 $A$ ) 和 $E_2$ (对于 $B$ ) 之一的元素. 图 5.6 中阴影区域表示对称差.

$◼$ $\{1,2,3,4\}△\{3,4,5\}=\{1,2,5\}$ .

(3)两个集合的笛卡儿积 两个集合的笛卡儿积由

$$\begin{array}{}\text{(5.65a)}& A\times B=\{\left(a,b\right)\mid a\in A\wedge b\in B\}\end{array}$$

定义. $A\times B$ 的元素(a, b)称为有序对,并且由

$$\begin{array}{}\text{(5.65b)}& \left(a,b\right)=\left(c,d\right)\iff a=c\vee b=d\end{array}$$

刻画. 两个有限集的笛卡儿积的元素个数等于

$$\begin{array}{}\text{(5.65c)}& \mathrm{card}\left(A\times B\right)=\left(\mathrm{card}A\right)\left(\mathrm{card}B\right).\end{array}$$

$◼\mathbf{A}$: 对于 $A=\{1,2,3\}$ 和 $B=\{2,3\}$ ,我们得到

$$A\times B=\{\left(1,2\right),\left(1,3\right),\left(2,2\right),\left(2,3\right),\left(3,2\right),\left(3,3\right)\},$$

以及

$$B\times A=\{\left(2,1\right),\left(2,2\right),\left(2,3\right),\left(3,1\right),\left(3,2\right),\left(3,3\right)\},$$

并且 $\mathrm{card}A=3,\mathrm{card}B=2,\mathrm{card}\left(A\times B\right)=\mathrm{card}\left(B\times A\right)=6$ .

$◼\mathbf{B}$: $x,y$ 平面的每个点可以用笛卡儿积 $\mathbb{R}\times \mathbb{R}\left(\mathbb{R}\text{是实数集) 定义. 坐标}x,y\text{的}\right)$ 集用 $\mathbb{R}\times \mathbb{R}$ 表示,所以

$${\mathbb{R}}^2=\mathbb{R}\times \mathbb{R}=\{\left(x,y\right)\mid x\in \mathbb{R},y\in \mathbb{R}\}.$$

(4) $n$ 个集合的笛卡儿积 固定序列的一种次序 (第一个元素,第二个元素, $\cdots$ , 第 $n$ 个元素),可由 $n$ 个元素定义一个有序 $n$ 组. 如果 $a_i\in A_i\left(i=1,2,\cdots ,n\right)$ 是这些元素,那么记 $n$ 组为 $\left(a_1,a_2,\cdots ,a_n\right)$ ,其中 $a_i$ 称为第 $i$ 个分量.

对于 $n=3,4,5$ ,这些 $n$ 组称为三元组、四元组、五元组.

$n$ 项笛卡儿积 $A_1\times A_2\times \cdots \times A_n$ 是所有有序 $n$ 组 $\left(a_1,a_2,\cdots ,a_n\right)$ (其中 $a_i\in A_i)$ 的集合:

$$\begin{array}{}\text{(5.66a)}& A_1\times A_2\times \cdots \times A_n=\left\{\left(a_1,a_2,\cdots ,a_n\right)\mid a_i\in A_i\left(i=1,\cdots ,n\right)\right\}.\end{array}$$

如果每个 $A_i$ 都是有限集,那么有序 $n$ 组的个数是

$$\begin{array}{}\text{(5.66b)}& \mathrm{card}\left(A_1\times A_2\times \cdots \times A_n\right)=\mathrm{card}{A}_1\mathrm{card}{A}_2\cdots \mathrm{card}{A}_n.\end{array}$$

注 集合 $A$ 与其自身的 $n$ 次笛卡儿积记作 $A^n$ .