3.4.3 球面三角形的计算

3.4.3.1 基本问题、精度评估

这里所谓的基本问题是指球面三角形计算中最常出现的各种情形. 对于锐角球面三角形来说, 有好几种方法去求解每个基本问题, 这取决于计算是否仅基于公式 (3.187a) 至 (3.191b), 或者还基于公式 (3.192a) 至 (3.201), 以及只求该三角形的一个量还是多个量.

包含正切函数的公式在数值上可以得到更精确的结果, 尤其是相比于该数值接近于 $90^{\circ}$ 时用正弦函数确定它和该数值接近于 $0^{\circ}$ 或 $180^{\circ}$ 时用余弦函数确定它. 对于欧拉三角形来说, 用正弦定律计算的量有两个值, 因为正弦函数在两个第一象限中都取正, 而从其他函数得到的结果是唯一的.

3.4.3.2 直角球面三角形

1. 专门公式

在直角球面三角形中至少有一个角是 $90^{\circ}$ . 边和角的记法类似于平面直角三角形. 如果像图 3.96 那样 $γ$ 是一个直角,则边 $c$ 称为斜边, $a$ 和 $b$ 称为直角边, $α$ 和 $β$ 称为侧角. 对于 $γ = 90^{\circ}$ 从等式 (3.187d) 至 (3.191b) 推出:

\begin{matrix} (3.202a) & \sin a = \sin α \sin c, \end{matrix}

\begin{matrix} (3.202b) & \sin b = \sin β \sin c, \end{matrix}

\begin{matrix} (3.202c) & \cos c = \cos a \cos b, \end{matrix}

\begin{matrix} (3.202d) & \cos c = \cot α \cot β, \end{matrix}

\begin{matrix} (3.202e) & \tan a = \cos β \tan c, \end{matrix}

\begin{matrix} (3.202f) & \tan b = \cos α \tan c, \end{matrix}

\begin{matrix} (3.202g) & \tan b = \sin a \tan β, \end{matrix}

\begin{matrix} (3.202h) & \tan a = \sin b \tan α, \end{matrix}

\begin{matrix} (3.202i) & \cos α = \sin β \cos a, \end{matrix}

\begin{matrix} (3.202j) & \cos β = \sin α \cos b . \end{matrix}

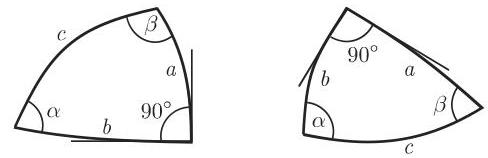
01935d9a-00b5-7750-94cb-0c4c22581c4c_226_576_604_488_158_0.jpg

如果在一些问题中给定了其他的边或角,例如量 $b, γ, α$ 而不是 $α, β, γ$ ,则可以通过这些量的轮换得到必需的等式. 对于直角球面三角形中的计算, 通常从三个已知量 $(γ = 90^{\circ}$ 和两个其他的量) 开始. 表 3.8 表示存在着的六个基本问题.

基本问题	已知的确定量	确定其余的量所需公式的编号
(1)	斜边和一直角边 $c, a$	$α (3.202 a), β (3.202 e), b (3.202 c)$
(2)	两直角边 $a, b$	$α (3.202 h), β (3.202 g), c (3.202 c)$
(3)	斜边和一个角 $c, α$	$a (3.202 a), b (3.202 f), β (3.202 d)$
(4)	一直角边和其上的角 $a, β$	$c (3.202 e), b (3.202 j), α (3.202 i)$
(5)	一直角边和其所对的角 $a, α$	$b (3.202 h), c (3.202 a), β (3.202 i)$
(6)	两个角 $α, β$	$a (3.202 i), b (3.202 j), c (3.202 d)$

2. 纳皮尔法则

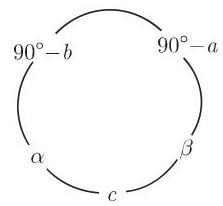
等式 (3.202a)-(3.202j) 可以概括成纳皮尔法则. 如果一个直角球面三角形的五个确定的量 (不算直角) 按它们在三角形中同样的顺序沿一个圆排列, 并将直角边替换为它们的余角 $90^{\circ} - a, 90^{\circ} - b$ (图 3.97),则以下事实成立:

(1)每个确定的量的余弦等于其相邻的量的余切值之积.

(2)每个确定的量的余弦等于其不相邻的量的正弦值之积.

01935d9a-00b5-7750-94cb-0c4c22581c4c_226_709_1556_223_206_0.jpg

$◼ A$ : $\cos α = \cot (90^{\circ} - b) \cot c = \frac{\tan b}{\tan c}$ (见(3.202f)).

$◼ B$ : $\cos (90^{\circ} - a) = \sin c \sin α = \sin a$ (见 (3.202a)).

$◼ C$ : 将球的经纬线绘制在沿中央子午线与球相切的圆柱体上. 该子午线与赤道构成了高斯-克吕格坐标系的坐标轴 (图 3.98(a),(b)).

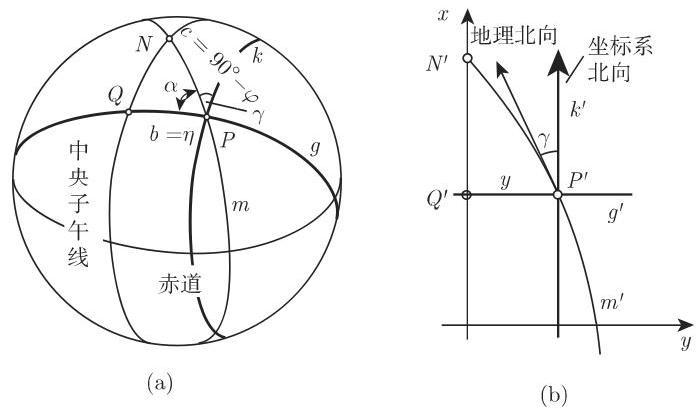
01935d9a-00b5-7750-94cb-0c4c22581c4c_227_472_593_699_411_0.jpg

解球面上的一点 $P$ 将对应于平面上的点 $P^{'}$ . 通过点 $P$ 垂直于中央子午线的大圆 $g$ 映射成垂直于 $x$ 轴的一条直线 $g^{'}$ ,而过 $P$ 点平行于给定子午线的小圆 $k$ 成为平行于 $x$ 轴的直线 $k^{'}$ (格网子午线). 通过 $P$ 点的子午线 $m$ 的像不是直线而是一条曲线 $m^{'}$ (真实子午线). $P^{'}$ 处 $m^{'}$ 的切线向上的方向给出地理北向, $k^{'}$ 向上的方向给出坐标系北向. 两个北向之间的夹角 $γ$ 称为子午线收敛角.

在 $c = 90^{\circ} - φ, b = η$ 的直角球面三角形 $Q P N$ 中,可以从 $α = 90^{\circ} - γ$ 得到 $γ$ . 纳皮尔法则给出 $\cos α = \frac{\tan b}{\tan c}$ 或 $\cos (90^{\circ} - γ) = \frac{\tan η}{\tan (90^{\circ} - φ)}, \sin γ = \tan η \tan φ$ . 因为 $γ$ 和 $η$ 非常小,故可以认为 $\sin γ \approx γ, \tan η \approx η$ ; 于是 $γ = η \tan φ$ 成立. 对于很小的距离 $η$ 这个圆柱体图的长度偏差也非常小,因此可以替换 $η = \frac{y}{R}$ ,其中 $y$ 是 $P$ 的纵坐标. 由此得 $γ = (\frac{y}{R}) \tan φ$ . 对于 $φ = 50^{\circ}, y = 100$ 千米,得出子午线收敛角 $γ = 0.018706$ 或将 $γ$ 从弧度转换成角度,得 $γ = 1^{\circ} 04^{'} 19^{''}$ .

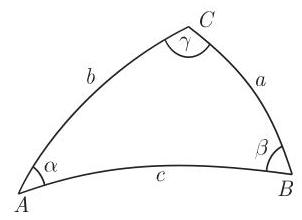
3.4.3.3 斜球面三角形

对于三个已知量, 要区分出六个基本问题, 正如在直角球面三角形时所做的那样. 角的记号是 $α, β, γ$ ,所对的边是 $a, b, c$ (图 3.99).

表 3.9~表 3.12 对应该用哪些公式来确定六个基本问题情形中的量进行了汇总. 问题 3 问题 6 也可以通过将一般三角形分解为两个直角三角形来解. 为此对于问题 3 和问题 4 (图 3.100,图 3.101) 可以使用从 $B$ 到 $A C$ 上 $D$ 点处的球面垂线, 而对于问题 5 和问题 6 (图 3.102) 则使用从 $C$ 到 $A B$ 上 $D$ 点的垂线.

01935d9a-00b5-7750-94cb-0c4c22581c4c_228_671_491_302_220_0.jpg

第一基本问题 SSS 已知: 3 边 $a, b, c$	第二基本问题 WWW 已知: 3 角 $α, β, γ$
条件:	条件:
$0^{\circ} < a + b + c < 360^{\circ},$	$180^{\circ} < α + β + γ < 540^{\circ}$ ,
$a + b > c, a + c > b, b + c > a$	$α + β < 180^{\circ} + γ, α + γ < 180^{\circ} + β,$
	$β + γ < 180^{\circ} + α$
解 1: 求 $α$ .	解 1: 求 $a$ .
$\cos α = \frac{\cos a - \cos b \cos c}{\sin b \sin c}$ 或	$\cos a = \frac{\cos α + \cos β \cos γ}{\sin β \sin γ}$ 或
$\tan \frac{α}{2} = \sqrt{\frac{\sin (s - b) \sin (s - c)}{\sin s \sin (s - a)}},$	$\cot \frac{a}{2} = \sqrt{\frac{\cos (σ - β) \cos (σ - γ)}{- \cos σ \cos (σ - α)}},$
$s = \frac{a + b + c}{2} .$	$σ = \frac{α + β + γ}{2} .$
解 2: 求 $α, β, γ$ .	解 2: 求 $a, b, c$ .
$k = \sqrt{\frac{\sin (s - a) \sin (s - b) \sin (s - c)}{\sin s}},$	$k^{'} = \sqrt{\frac{\cos (σ - α) \cos (σ - β) \cos (σ - γ)}{- \cos σ}} .$
$\tan \frac{α}{2} = \frac{k}{\sin (s - a)}, \tan \frac{β}{2} = \frac{k}{\sin (s - b)},$	$\cot \frac{a}{2} = \frac{k^{'}}{\cos (σ - α)}, \cot \frac{b}{2} = \frac{k^{'}}{\cos (σ - β)},$
$\tan \frac{γ}{2} = \frac{k}{\sin (s - c)} .$ 检验: $(s - a) + (s - b) + (s - c) = s$ ,	$\cot \frac{c}{2} = \frac{k^{'}}{\cos (σ - γ)} .$ 检验: $(σ - α) + (σ - β) + (σ - γ) = σ$ ,
$\tan \frac{α}{2} \tan \frac{β}{2} \tan \frac{γ}{2} \sin s = k$	$\cot \frac{a}{2} \cot \frac{b}{2} \cot \frac{c}{2} (- \cos σ) = k^{'}$

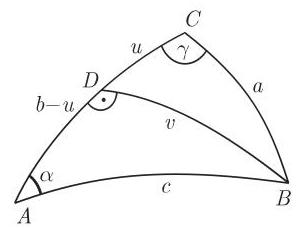
01935d9a-00b5-7750-94cb-0c4c22581c4c_228_476_1629_299_229_0.jpg

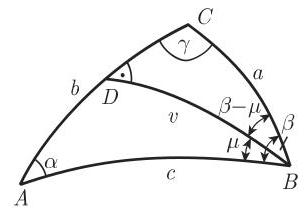
01935d9a-00b5-7750-94cb-0c4c22581c4c_228_950_1640_305_213_0.jpg

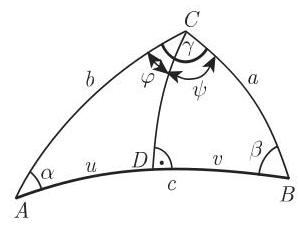
01935d9a-00b5-7750-94cb-0c4c22581c4c_229_671_491_300_226_0.jpg

第三基本问题已知: 2 边及其夹角,例如, $a, b, γ$
条件: 无
解 1: 求 $c$ ,或 $c$ 和 $α$ . $\cos c = \cos a \cos b + \sin a \sin b \cos γ,$ $\sin α = \frac{\sin a \sin γ}{\sin c} .$ $α$ 可以位于象限 I 或 II. 我们应用定理: 较大的角所对的边较大, 或检验计算: $\cos a - \cos b \cos c ≷ 0 \to \begin{array}{l} α 在象限 I . \\ α 在象限 I . \end{array}$ 解 2: 求 $α$ ,或 $α$ 和 $c$ . $\tan u = \tan a \cos γ$ $\tan α = \frac{\tan γ \sin u}{\sin (b - u)}$ $\tan c = \frac{\tan (b - u)}{\cos α} .$ 解 3: 求 $α$ 和 (或) $β$ . $\tan \frac{α + β}{2} = \frac{\cos \frac{a - b}{2}}{\cos \frac{a + b}{2}} \cot \frac{γ}{2}$	$\tan \frac{α - β}{2} = \frac{\sin \frac{a - b}{2}}{\sin \frac{a + b}{2}} \cot \frac{γ}{2}$ $(- 90^{\circ} < \frac{α - β}{2} < 90^{\circ})$ $α = \frac{α + β}{2} + \frac{α - β}{2}, β = \frac{α + β}{2} - \frac{α - β}{2} .$ 解 4: 求 $α, β, c$ . $\tan \frac{α + β}{2} = \frac{\cos \frac{a - b}{2} \cos \frac{γ}{2}}{\cos \frac{a + b}{2} \sin \frac{γ}{2}} = \frac{Z}{N},$ $\tan \frac{α - β}{2} = \frac{\sin \frac{a - b}{2} \cos \frac{γ}{2}}{\sin \frac{a + b}{2} \sin \frac{γ}{2}} = \frac{Z^{'}}{N^{'}}$ $(- 90^{\circ} < \frac{α + β}{2} < 90^{\circ})$ $α = \frac{α + β}{2} + \frac{α - β}{2}, β = \frac{α + β}{2} - \frac{α - β}{2},$ $\cos \frac{c}{2} = \frac{Z}{\sin \frac{α + β}{2}}, \sin \frac{c}{2} = \frac{Z^{'}}{\sin \frac{α - β}{2}} .$ 检验: 关于 $c$ 的双重计算

在表 3.9 至表 3.12 的表头中,已知边和已知角分别用 $S$ 和 $W$ 表示. 例如 $SWS$ 的意思是: 两边及其夹角是已知的.

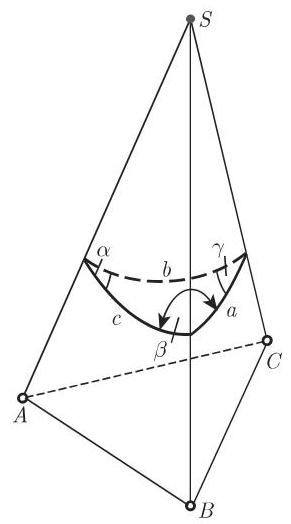
A 四面体一个四面体具有底 $A B C$ 和顶点 $S$ (图 3.103). 面 $A B S$ 和 $B C S$ 相互交成角 $β = 74^{\circ} 18^{'}, B C S$ 和 $C A S$ 交成角 $γ = 63^{\circ} 40^{'}, C A S$ 和 $A B S$ 交成角 $α =$ $80^{\circ} 00^{'}$ . 问 $A S, B S$ 和 $C S$ 每两个棱之间的夹角有多大?

解从围绕该棱锥顶点 $S$ 的一个球面,三面角 (图 3.103) 截出一个边为 $a, b$ , $c$ 的球面三角形.

侧面之间的夹角就是球面三角形的三个角, 所求棱之间的夹角是球面三角形的边. 确定角 $a, b, c$ 对应于第二基本问题. 由表 3.9 中的解 2 得

σ = 108^{\circ} 59^{'}, σ - α = 28^{\circ} 59^{'}, σ - β = 34^{\circ} 41^{'}, σ - γ = 45^{\circ} 19^{'},

k^{'} = 1.246983, \cot (\frac{a}{2}) = 1.425514, \cot (\frac{b}{2}) = 1.516440,

\cot (\frac{c}{2}) = 1.773328

解 1: 求 $γ$ 或 $γ$ 和 $a$ .

(- 90^{\circ} < \frac{a - b}{2} < 90^{\circ}),

a = \frac{a + b}{2} + \frac{a - b}{2}, b = \frac{a + b}{2} - \frac{a - b}{2} .

解 4: 求 $a, b, γ$ .

$\cos α + \cos β \cos γ ≷ 0 \to \begin{array}{l} α 在象限 1. \\ α 在象限 Π . \end{array}$

\tan \frac{a + b}{2} = \frac{\cos \frac{α - β}{2} \sin \frac{c}{2}}{\cos \frac{α + β}{2} \cos \frac{c}{2}} = \frac{Z}{N},

解 2: 求 $a$ 或 $a$ 和 $γ$ .

\tan \frac{a - b}{2} = \frac{\sin \frac{α - β}{2} \sin \frac{c}{2}}{\sin \frac{α + β}{2} \cos \frac{c}{2}} = \frac{Z^{'}}{N^{'}}

$\cot μ = \tan α \cos c, \tan a = \frac{\tan c \cos μ}{\cos (β - μ)},$

\tan γ = \frac{\cot (β - μ)}{\cos a} .

(90^{\circ} < \frac{a - b}{2} < 90^{\circ}),

解 3: 求 $a$ 和 (或) $b$ .

a = \frac{a + b}{2} + \frac{a - b}{2}, b = \frac{a + b}{2} - \frac{a - b}{2},

\tan \frac{a + b}{2} = \frac{\cos \frac{α - β}{2}}{\cos \frac{α + β}{2}} \tan \frac{c}{2},

\sin \frac{γ}{2} = \frac{Z}{\sin \frac{a + b}{2}}, \cos \frac{γ}{2} = \frac{Z^{'}}{\sin \frac{a - b}{2}} .

\tan \frac{a - b}{2} = \frac{\sin \frac{α - β}{2}}{\sin \frac{α + β}{2}} \tan \frac{c}{2}

检验: 关于 $γ$ 的双重计算

第五基本问题 SS 已知: 2 边和其中之一所对的角,例如, $a, b, α$	已知: 2 角和其中之一所对的边,例如 $, a, α, β$
条件: 见分情况讨论.	条件: 见分情况讨论.
解: 所求为任何缺失的量.	解: 所求为任何缺失的量.
$\sin β = \frac{\sin b \sin α}{\sin a}$ 可能有 2 个值 $β_{1}, β_{2}$ . 设 $β_{1}$ 是锐角而 $β_{2} = 180^{\circ} - β_{1}$ 是钝角.	$\sin b = \frac{\sin a \sin β}{\sin α}$ 可能有 2 个值 $b_{1}, b_{2}$ . 设 $b_{1}$ 是锐角而 $b_{2} = 180^{\circ} - b_{1}$ 是钝角.
分情况讨论:	分情况讨论:
$\frac{\sin b \sin α}{\sin a} > 1 0$ 个解. 2. $\frac{\sin b \sin α}{\sin a} = 1 1$ 个解 $β = 90^{\circ}$ . 3. $\frac{\sin b \sin α}{\sin a} < 1$ : 3.1. $\sin a > \sin b$ :	$\frac{\sin a \sin β}{\sin α} > 1 0$ 个解. 2. $\frac{\sin a \sin β}{\sin α} = 1 1$ 个解 $b = 90^{\circ}$ . 3. $\frac{\sin a \sin β}{\sin α} < 1$ : 3.1. $\sin α > \sin β$ .
3.1.1. $b < 90^{\circ} 1$ 个解 $β_{1}$ .	3.1.1. $β < 90^{\circ} 1$ 个解 $b_{1}$ .
3.1.2. $b > 90^{\circ} 1$ 个解 $β_{2}$ .	3.1.2. $β > 90^{\circ} 1$ 个解 $b_{2}$ .
3.2. $\sin a < \sin b$ :	3.2. $\sin α < \sin β$ :
3.2.1. $\begin{array}{l} a < 90^{\circ}, α < 90^{\circ} \\ a > 90^{\circ}, α > 90^{\circ} \end{array}} \begin{array}{l} 2 个解 \\ β_{1}, β_{2} . \end{array}$	3.2.1. $\begin{array}{l} a < 90^{\circ}, α < 90^{\circ} \\ a > 90^{\circ}, α > 90^{\circ} \end{array}} \begin{array}{l} 2 个解 \\ b_{1}, b_{2} . \end{array}$
3.2.2. $\begin{array}{l} a < 90^{\circ}, α > 90^{\circ} \\ a > 90^{\circ}, α < 90^{\circ} \end{array}} 0$ 个解.	$\begin{array}{l} a < 90^{\circ}, α > 90^{\circ} \\ a > 90^{\circ}, α < 90^{\circ} \end{array}} 0$ 个解.
用一个角或用两个角 $β$ 做进一步计算:	用一条边或用两条边 $b$ 做进一步计算:

方法 2

检验: 关于 $\frac{c}{2}$ 和 $\frac{γ}{2}$ 的双重计算

01935d9a-00b5-7750-94cb-0c4c22581c4c_232_678_491_291_524_0.jpg

$◼ B$ : 无线电定向在无线电定向的例子中,两个固定站点 $P_{1} (λ_{1}, φ_{1})$ 和 $P_{2} (λ_{2}, φ_{2})$ 接收一条船通过无线电波发射的方位角 $δ_{1}$ 和 $δ_{2}$ (图 3.104). 这项任务就是要确定船的位置 $P_{0}$ 的地理坐标. 该问题在航海学中以岸对船定向著称,是球上的一种交会问题, 解法上与平面中的交会问题类似 (参见第 196 页 3.2.2.3).

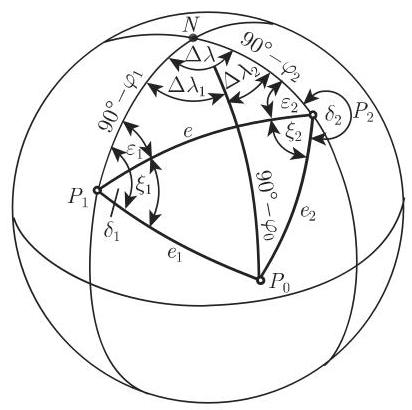
01935d9a-00b5-7750-94cb-0c4c22581c4c_232_617_1269_412_410_0.jpg

(1) 三角形 $P_{1} P_{2} N$ 中的计算在三角形 $P_{1} P_{2} N$ 中边 $P_{1} N = 90^{\circ} - φ_{1}, P_{2} N =$ $90^{\circ} - φ_{2}$ 和角 $≪ P_{1} N P_{2} = λ_{2} - λ_{1} = Δ λ$ 已知. 角 $≪ ε_{1}, ε_{2}$ 和线段的 $P_{1} P_{2} = e$ 的计算对应于第三基本问题.

(2) 三角形 $P_{1} P_{2} P_{0}$ 中的计算因为 $ξ_{1} = δ_{1} - ε_{1}, ξ_{2} = 360^{\circ} - (δ_{2} + ε_{2})$ ,所以边 $e$ 及它上面的角 $ξ_{1}$ 和 $ξ_{2}$ 在 $P_{1} P_{0} P_{2}$ 中是已知的. 边 $e_{1}$ 和 $e_{2}$ 的计算,对应于第四基本问题,解 3. 点 $P_{0}$ 的坐标可以从方位角和它到 $P_{1}$ 或 $P_{2}$ 的距离计算出来.

(3) 三角形 $N P_{1} P_{0}$ 中的计算在三角形 $N P_{1} P_{0}$ 中有已知的两条边 $N P_{1} =$ $90^{\circ} - φ_{1}, P_{1} P_{0} = e_{1}$ 及夹角 $δ_{1}$ . 边 $N P_{0} = 90^{\circ} - φ_{0}$ 和角 $Δ λ_{1}$ 按照第三基本问题,解 1 计算. 为了检验,可以在三角形 $N P_{0} P_{2}$ 中再次计算 $N P_{0} = 90^{\circ} - φ_{0}$ ,还有 $Δ λ_{2}$ . 于是,点 $P_{0}$ 的经度 $λ_{0} = λ_{1} + Δ λ_{1} = λ_{2} - Δ λ_{2}$ 和纬度 $φ_{0}$ 就知道了.

3.4.3.4 球面曲线

球面三角学在航海中有非常重要的应用. 一个基本问题是确定航向角, 它给出最优的航线. 其他的应用领域是大地勘测以及机器人运动设计.

1. 大圆航线

(1) 概念 球表面的测地线 - 它是曲线,是连接 $A$ 和 $B$ 两点的最短路径——被称为大圆航线或大圆 (参见第 213 页 3.4.1.1, 3.).

(2) 大圆航线的方程 沿大圆航线 - 除子午线和赤道外 - 运动需要航向角的连续变化. 这些具有与位置有关的航向角 $α$ 的大圆航线可以通过它们最接近北极的点 $P_{N} (λ_{N}, φ_{N})$ 唯一给出,其中 $φ_{N} > 0^{\circ}$ . 大圆航线在最接近北极的点具有航向角 $α_{N} = 90^{\circ}$ . 根据图 3.105 利用纳皮尔法则 (参见第 227 页 3.4.3.2,2.),可以给出通过 $P_{N}$ 和运行点 $Q (λ_{Q}, φ_{Q})$ (它与 $P_{N}$ 的相对位置是任意的) 的大圆航线方程, 为

\begin{matrix} (3.203) & \tan φ_{N} \cos (λ_{Q} - λ_{N}) = \tan φ_{Q} . \end{matrix}

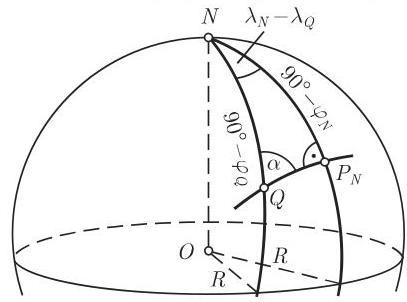
01935d9a-00b5-7750-94cb-0c4c22581c4c_233_617_1284_407_302_0.jpg

最接近北极的点在点 $A (λ_{A}, φ_{A}) (φ_{A} \neq 90^{\circ})$ 处具有航向角 $α_{A} (α_{A} \neq 0^{\circ})$ 的大圆航线最接近北极的点 $P_{N} (λ_{N}, φ_{N})$ 的坐标,可以根据图 3.106 考虑 $P_{N}$ 的相对位置和 $α_{A}$ 的符号利用纳皮尔法则来计算:

\begin{matrix} (3.204a) & φ_{N} = \arccos (\sin | α_{A} | \cos φ_{A}) \end{matrix}

和

\begin{matrix} (3.204b) & λ_{N} = λ_{A} + sign (α_{A}) | \arccos \frac{\tan φ_{A}}{\tan φ_{N}} | . \end{matrix}

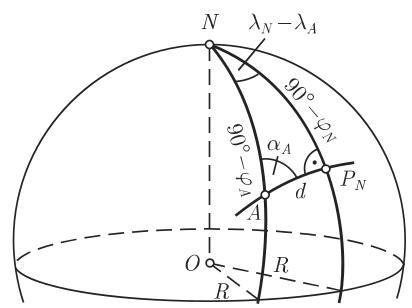
01935d9a-00b5-7750-94cb-0c4c22581c4c_234_616_488_412_308_0.jpg

评论如果计算出来的地理距离 $λ$ 不在 $- 180^{\circ} < λ \leq 180^{\circ}$ 内,则对于 $λ \neq$ $\pm k \cdot 180^{\circ} (k \in N)$ 简化的地理距离 $λ_{red}$ 是

\begin{matrix} (3.205) & λ_{red} = 2 \arctan (\tan \frac{λ}{2}) . \end{matrix}

这称为角在定义域内的简化.

与赤道的交点大圆航线与赤道的交点 $P_{E_{1}} (λ_{E_{1}}, 0^{\circ})$ 和 $P_{E_{2}} (λ_{E_{2}}, 0^{\circ})$ 可以由 (3.203) 计算,因为 $\tan φ_{N} \cos (λ_{E_{ν}} - λ_{N}) = 0 (ν = 1, 2)$ 必须满足:

\begin{matrix} (3.206) & λ_{E_{ν}} = λ_{N} \mp 90^{\circ} (ν = 1, 2) . \end{matrix}

评论在某些情形中需要根据 (3.205) 来做角的简化.

(3) 弧长 如果大圆航线通过点 $A (λ_{A}, φ_{A})$ 和 $B (λ_{B}, φ_{B})$ ,则由边的余弦定律得出球面距离 $d$ 或两点之间的弧长:

\begin{matrix} (3.207a) & d = \arccos [\sin φ_{A} \sin φ_{B} + \cos φ_{A} \cos φ_{B} \cos (λ_{B} - λ_{A})] . \end{matrix}

要是考虑地球半径 $R$ ,则这个圆心角可以换算成长度:

\begin{matrix} (3.207b) & d = \arccos [\sin φ_{A} \sin φ_{B} + \cos φ_{A} \cos φ_{B} \cos (λ_{B} - λ_{A})] \cdot \frac{π R}{180^{\circ}} . \end{matrix}

(4) 航向角 使用边的正弦定律和余弦定律计算 $\sin α_{A}$ 和 $\cos α_{A}$ ,相除后给出航向角 $α_{A}$ 的最终结果:

\begin{matrix} (3.208) & α_{A} = \arctan \frac{\cos φ_{A} \cos φ_{B} \sin (λ_{B} - λ_{A})}{\sin φ_{B} - \sin φ_{A} \cos d} . \end{matrix}

评论利用公式 (3.207a),(3.208),(3.204a) 和 (3.204b),对于由两点 $A$ 和 $B$ 给出的大圆航线可以计算出最接近北极的点 $P_{N}$ 的坐标.

(5) 与平行圆的交点 关于大圆航线与平行圆 $φ = φ_{X}$ 的交点 $X_{1} (λ_{X_{1}}, φ_{X})$ 和 $X_{2} (λ_{X_{2}}, φ_{X})$ ,我们从 (3.203) 得

\begin{matrix} (3.209) & λ_{X_{ν}} = λ_{N} \mp \arccos \frac{\tan φ_{X}}{\tan φ_{N}} (ν = 1, 2) . \end{matrix}

从对两个交角 $α_{X_{1}}$ 和 $α_{X_{2}}$ (在那里具有最接近北极的点 $P_{N} (λ_{N}, φ_{N})$ 的大圆航线与平行圆 $φ = φ_{X}$ 相交) 所用的纳皮尔法则,得

\begin{matrix} (3.210) & | α_{X_{ν}} | = \arcsin \frac{\cos φ_{N}}{\cos φ_{X}} (ν = 1, 2) . \end{matrix}

对于最小的航向角 $| α_{min} |$ 来说,反正弦函数的自变量一定是关于变量 $φ_{X}$ 的极值. 由此得到: $\sin φ_{X} = 0 \Rightarrow φ_{X} = 0$ ,即航向角的绝对值在与赤道交点处最小:

\begin{matrix} (3.211) & | α_{X_{min}} | = 90^{\circ} - φ_{N} . \end{matrix}

评论 1 (3.209) 的解仅当 $| φ_{X} | \leq φ_{N}$ 时存在.

评论 2 在某些情形中需要根据 (3.205) 进行角的简化.

(6) 与子午线的交点 根据 (3.203),大圆航线与子午线 $λ = λ_{Y}$ 的交点 $Y (λ_{Y}, φ_{Y})$ 由下式给出

\begin{matrix} (3.212) & φ_{Y} = \arctan [\tan φ_{N} \cos (λ_{Y} - λ_{N})] . \end{matrix}

2. 小圆

(1) 概念 这里, 需要比在第 213 页 3.4.1.1 中更加精确的球面上小圆的定义: 小圆是球面上与固定点 $M (λ_{M}, φ_{M})$ 的球面距离为 $r (r < 90^{\circ})$ 的点的轨迹 (图 3.107). 用 $M$ 表示小圆的球面中心; $r$ 称为小圆的球面半径.

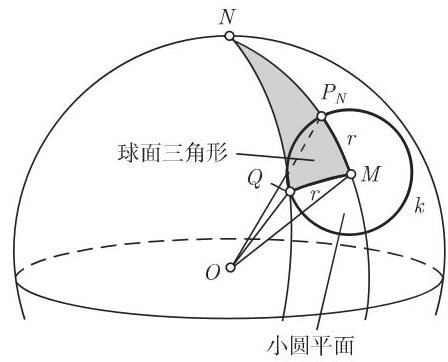
01935d9a-00b5-7750-94cb-0c4c22581c4c_235_596_1254_448_362_0.jpg

小圆平面是高为 $h$ 的球冠的底 (参见第 207 页 3.3.4). 球面中心 $M$ 位于小圆平面上的小圆圆心上方. 在这个平面上小圆的平面半径是 $r_{0}$ (图 3.108). 因此,平行圆是具有 $φ_{M} = \pm 90^{\circ}$ 的特殊小圆.

$◼$ 当 $r \to 90^{\circ}$ 时小圆趋向于大圆航线.

(2) 小圆的方程 作为定义参数,要么使用 $M$ 和 $r$ ,要么使用最接近北极的小圆上的点 $P_{N} (λ_{N}, φ_{N})$ 和 $r$ . 如果小圆上的运行点是 $Q (λ, φ)$ ,那么根据图 3.107 利用关于边的余弦定律我们可以得到小圆的方程:

\begin{matrix} (3.213a) & \cos r = \sin φ \sin φ_{M} + \cos φ \cos φ_{M} \cos (λ - λ_{M}) . \end{matrix}

因为 $φ_{M} = φ_{N} - r$ 且 $λ_{M} = λ_{N}$ ,由此得

\begin{matrix} (3.213b) & \cos r = \sin φ \sin (φ_{N} - r) + \cos φ \cos (φ_{N} - r) \cos (λ - λ_{N}) . \end{matrix}

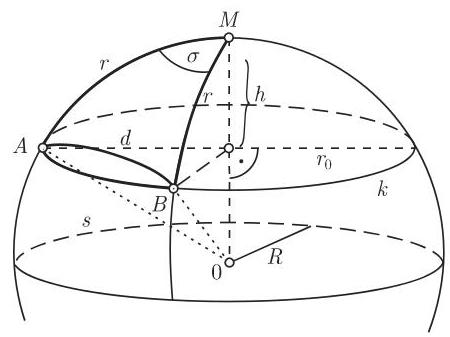
01935d9a-00b5-7750-94cb-0c4c22581c4c_236_596_731_450_337_0.jpg

$◼ A$ : 当 $φ_{M} = 90^{\circ}$ 时,因为 $\cos r = \sin φ \Rightarrow \sin (90^{\circ} - r) = \sin φ \Rightarrow φ =$ 常数,所以由 (3.213a) 得到平行圆.

$◼ B$ : 当 $r \to 90^{\circ}$ 时,由 (3.213b) 推出大圆航线.

(3) 弧长 小圆 $k$ 上两点 $A (λ_{A}, φ_{A})$ 和 $B (λ_{B}, φ_{B})$ 之间的弧长 $s$ 可以根据图 3.108 由等式 $\frac{s}{σ} = \frac{2 π r_{0}}{360^{\circ}}, \cos d = \cos^{2} r + \sin^{2} r \cos σ$ 和 $r_{0} = R \sin r$ 计算:

\begin{matrix} (3.214) & s = \sin r \arccos \frac{\cos d - \cos^{2} r}{\sin^{2} r} \cdot \frac{π R}{180^{\circ}} . \end{matrix}

$◼$ 当 $r \to 90^{\circ}$ 时小圆成为大圆航线,从 (3.214) 和 (3.207b) 推出 $s = d$ .

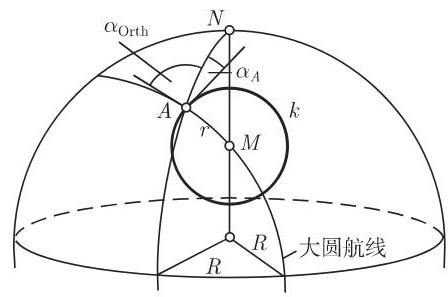
(4) 航向角 根据图 3.109,通过 $A (λ_{A}, φ_{A})$ 和 $M (λ_{M}, φ_{M})$ 的大圆航线与半径为 $r$ 的小圆垂直相交. 对于大圆航线的航向角 $α_{Orth}$ 来说,据 (3.208) 有

\begin{matrix} (3.215a) & α_{Orth} = \arctan \frac{\cos φ_{A} \cos φ_{M} \sin (λ_{M} - λ_{A})}{\sin φ_{M} - \sin φ_{A} \cos r}, \end{matrix}

因此,我们得到所求的小圆在点 $A$ 处的航向角 $α_{A}$ :

\begin{matrix} (3.215b) & α_{A} = (| α_{Orth} | - 90^{\circ}) sign (α_{Orth}) . \end{matrix}

(5) 与平行圆的交点 关于小圆与平行圆 $φ = φ_{X}$ 交点 $X_{1} (λ_{X_{1}}, φ_{X})$ 和 $X_{2}$ $(λ_{X_{2}}, φ_{X})$ 的地理经度,我们从 (3.213a) 推得

\begin{matrix} (3.216) & λ_{X_{ν}} = λ_{M} \mp \arccos \frac{\cos r - \sin φ_{X} \sin φ_{M}}{\cos φ_{X} \cos φ_{M}} (ν = 1, 2) . \end{matrix}

评论在某些情形中需要根据 (3.205) 进行角的简化.

01935d9a-00b5-7750-94cb-0c4c22581c4c_237_596_551_448_297_0.jpg

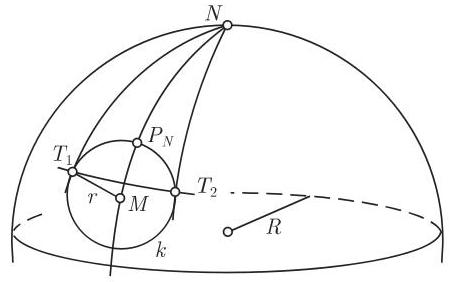
(6) 切点 在切点 $T_{1} (λ_{T_{1}}, φ_{T})$ 和 $T_{2} (λ_{T_{2}}, φ_{T})$ 处,小圆与两条子午线,即切向子午线相接触 (图 3.110). 因为对它们而言, (3.216) 中反余弦函数的自变量一定是关于变量 $φ_{X}$ 的极值,所以有

\begin{matrix} (3.217a) & φ_{T} = \arcsin \frac{\sin φ_{M}}{\cos r}, \end{matrix}

\begin{matrix} (3.217b) & λ_{T_{ν}} = λ_{M} \mp \arccos \frac{\cos r - \sin φ_{X} \sin φ_{M}}{\cos φ_{X} \cos φ_{M}} (ν = 1, 2) . \end{matrix}

01935d9a-00b5-7750-94cb-0c4c22581c4c_237_598_1181_451_282_0.jpg

评论在某些情形中需要根据 (3.205) 进行角的简化.

(7) 与子午线的交点 小圆与子午线 $λ = λ_{Y}$ 的交点 $Y_{1} (λ_{Y}, φ_{Y_{1}})$ 和 $Y_{2} (λ_{Y},$ $φ_{Y_{2}})$ 的地理纬度可以根据 (3.213a) 利用等式

\begin{matrix} (3.218a) & φ_{Y_{ν}} = \arcsin \frac{- A C \pm B \sqrt{A^{2} + B^{2} - C^{2}}}{A^{2} + B^{2}} (ν = 1, 2), \end{matrix}

来计算, 其中用到了以下记号:

\begin{matrix} (3.218b) & A = \sin φ_{M}, B = \cos φ_{M} \cos (λ_{Y} - λ_{M}), C = - \cos r . \end{matrix}

一般来说,对于 $A^{2} + B^{2} > C^{2}$ ,存在两个不同的解,而如果极点在小圆上,则会丢掉一个.

如果 $A^{2} + B^{2} = C^{2}$ 成立并且没有极点在小圆上,则子午线在具有地理纬度 $φ_{Y_{1}} = φ_{Y_{2}} = φ_{T}$ 的切点处与小圆相切.

3. 斜航线

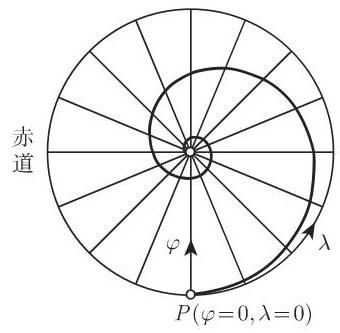
(1) 概念 以相同航向角与所有子午线相交的一条球面曲线称为斜航线或球面螺旋线. 因此纬线 $(α = 90^{\circ})$ 和子午线 $(α = 0^{\circ})$ 是特殊的斜航线.

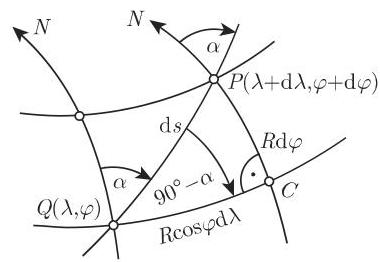
(2) 斜航线的方程 图 3.111 显示的是以航向角 $α$ 通过运行点 $Q (λ, φ)$ 和无限接近的点 $P (λ + d λ, φ + d φ)$ 的斜航线. 直角球面三角形 $Q C P$ 因为很小所以可以看成平面三角形. 于是有

\begin{matrix} (3.219a) & \tan α = \frac{R \cos φ d λ}{R d φ} \Rightarrow d λ = \frac{\tan α d φ}{\cos φ} . \end{matrix}

01935d9a-00b5-7750-94cb-0c4c22581c4c_238_630_926_380_262_0.jpg

考虑到斜航线必须通过点 $A (λ_{A}, φ_{A})$ ,因此利用积分推出斜航线的方程:

\begin{matrix} (3.219b) & λ - λ_{A} = \tan α \ln \frac{\tan (45^{\circ} + \frac{φ}{2})}{\tan (45^{\circ} + \frac{φ_{A}}{2})} \cdot \frac{180^{\circ}}{π} (α \neq 90^{\circ}) . \end{matrix}

特别当 $A$ 是斜航线与赤道的交点 $P_{E} (λ_{E}, 0^{\circ})$ 时,则有

\begin{matrix} (3.219c) & λ - λ_{E} = \tan α \ln \tan (45^{\circ} + \frac{φ}{2}) \cdot \frac{180^{\circ}}{π} (α \neq 90^{\circ}) . \end{matrix}

评论可以利用 (3.224) 计算 $λ_{E}$ .

(3) 弧长 从图 3.111 我们可以看出微分关系

\begin{matrix} (3.220a) & \cos α = \frac{R d φ}{d s} \Rightarrow d s = \frac{R d φ}{\cos α} . \end{matrix}

关于 $φ$ 积分,得端点为 $A (λ_{A}, φ_{A})$ 和 $B (λ_{B}, φ_{B})$ 的弧段的弧长 $s$ :

\begin{matrix} (3.220b) & s = \frac{| φ_{B} - φ_{A} |}{\cos α} \cdot \frac{π R}{180^{\circ}} (α \neq 90^{\circ}) . \end{matrix}

如果 $A$ 是起点, $B$ 是终点,则从给定的值 $A, α$ 和 $s$ 出发可以根据 (3.220b) 逐步地先计算出 $φ_{B}$ ,然后再根据 (3.219b) 计算出 $λ_{B}$ .

近似公式根据图 3.111,设 $Q = A$ 和 $P = B$ ,我们利用地理纬度的算术平均值以及 (3.221a) 和 (3.221b) 可以得到弧长 $l$ 的近似值:

\begin{matrix} (3.221a) & \sin α = \frac{\cos \frac{φ_{A} + φ_{B}}{2} (λ_{B} - λ_{A})}{l} \cdot \frac{π R}{180^{\circ}} . \end{matrix}

\begin{matrix} (3.221b) & l = \frac{\cos \frac{φ_{A} + φ_{B}}{2}}{\sin α} (λ_{B} - λ_{A}) \cdot \frac{π R}{180^{\circ}} . \end{matrix}

(4) 航向角 根据 (3.219b) 和 (3.219c),对于通过点 $A (λ_{A}, φ_{A})$ 和 $B (λ_{B}, φ_{B})$ , 或者通过点 $A (λ_{A}, φ_{A})$ 和它与赤道交点 $P_{E} (λ_{E}, 0^{\circ})$ 的斜航线的航向角 $α$ ,下列公式成立:

\begin{matrix} (3.222a) & \begin{matrix} α = \arctan \frac{(λ_{B} - λ_{A})}{\tan \frac{\tan (45^{\circ} + \frac{φ_{B}}{2})}{\tan (45^{\circ} + \frac{φ_{A}}{2})}} \cdot \frac{π}{180^{\circ}}, \end{matrix} \end{matrix}

\begin{matrix} (3.222b) & α = \arctan \frac{(λ_{A} - λ_{E})}{\ln \tan (45^{\circ} + \frac{φ_{A}}{2})} \cdot \frac{π}{180^{\circ}} . \end{matrix}

(5) 与平行圆的交点 假设斜航线以航向角 $α$ 通过点 $A (λ_{A}, φ_{A})$ . 斜航线与平行圆 $φ = φ_{X}$ 交点 $X (λ_{X}, φ_{X})$ 由(3.219b)计算:

\begin{matrix} (3.223) & λ_{X} = λ_{A} + \tan α \cdot \ln \frac{\tan (45^{\circ} + \frac{φ_{X}}{2})}{\tan (45^{\circ} + \frac{φ_{A}}{2})} \cdot \frac{180^{\circ}}{π} (α \neq 90^{\circ}) . \end{matrix}

利用 (3.223) 计算与赤道的交点 $P_{E} (λ_{E}, 0^{\circ})$ 得

\begin{matrix} (3.224) & λ_{E} = λ_{A} - \tan α \cdot \ln \tan (45^{\circ} + \frac{φ_{A}}{2}) \cdot \frac{180^{\circ}}{π} (α \neq 90^{\circ}) . \end{matrix}

评论在某些情形中需要根据 (3.205) 进行角的简化.

(6) 与子午线的交点 斜航线——除平行圆和子午线外——以螺旋形环绕极点 (图 3.112). 以航向角 $α$ 通过点 $A (λ_{A}, φ_{A})$ 的斜航线与子午线 $λ = λ_{Y}$ 的无穷多交点 $Y_{ν} (λ_{Y}, φ_{Y_{ν}}) (ν \in Z)$ 可以由(3.219b)计算出来:

φ_{Y_{ν}} = 2 \arctan {\exp [\frac{λ_{Y} - λ_{A} + ν \cdot 360^{\circ}}{\tan α} \cdot \frac{π}{180^{\circ}}]

\begin{matrix} (3.225) & \cdot \tan (45^{\circ} + \frac{φ_{A}}{2})} - 90^{\circ} (ν \in Z) . \end{matrix}

如果 $A$ 是斜航线的赤道交点 $P_{E} (λ_{E}, 0^{\circ})$ ,则简单地有

\begin{matrix} (3.226) & φ_{Y_{ν}} = 2 \arctan \exp [\frac{λ_{Y} - λ_{E} + ν \cdot 360^{\circ}}{\tan α} \cdot \frac{π}{180^{\circ}}] - 90^{\circ} (ν \in Z) . \end{matrix}

01935d9a-00b5-7750-94cb-0c4c22581c4c_240_652_494_340_333_0.jpg

4. 球面曲线的交点

(1)两条大圆航线的交点 假设所考虑的大圆航线具有最接近北极的点 $P_{N_{1}} (λ_{N_{1}}, φ_{N_{1}})$ 和 $P_{N_{2}} (λ_{N_{2}}, φ_{N_{2}})$ ,其中 $P_{N_{1}} \neq P_{N_{2}}$ 成立. 在两个大圆航线方程中代入交点 $S (λ_{S}, φ_{S})$ 给出方程组:

\begin{matrix} (3.227a) & \tan φ_{N_{1}} \cos (λ_{S} - λ_{N_{1}}) = \tan φ_{S}, \end{matrix}

\begin{matrix} (3.227b) & \tan φ_{N_{2}} \cos (λ_{S} - λ_{N_{2}}) = \tan φ_{S} . \end{matrix}

消去 $φ_{S}$ 并利用余弦函数的加法定律得

\begin{matrix} (3.228) & \tan λ_{S} = - \frac{\tan φ_{N_{1}} \cos λ_{N_{1}} - \tan φ_{N_{2}} \cos λ_{N_{2}}}{\tan φ_{N_{1}} \sin λ_{N_{1}} - \tan φ_{N_{2}} \sin λ_{N_{2}}} . \end{matrix}

方程 (3.228) 在地理经度的取值范围 $- 180^{\circ} < λ \leq 180^{\circ}$ 内有两个解 $λ_{S_{1}}$ 和 $λ_{S_{2}}$ . 相应的地理纬度可以从 (3.227a) 得到

\begin{matrix} (3.229) & φ_{S_{ν}} = \arctan [\tan φ_{N_{1}} \cos (λ_{S_{ν}} - λ_{N_{1}})] (ν = 1, 2) . \end{matrix}

交点 $S_{1}$ 和 $S_{2}$ 是对径点,即它们彼此是关于球心的镜像.

(2) 两条斜航线的交点 假设所考虑的斜航线具有赤道交点 $P_{E_{1}} (λ_{E_{1}}, 0^{\circ})$ 和 $P_{E_{2}} (λ_{E_{2}}, 0^{\circ})$ 以及航向角 $α_{1}$ 和 $α_{2} (α_{1} \neq α_{2})$ . 在两个斜航线方程中代入交点 $S (λ_{S}$ , $φ_{S})$ 给出方程组:

\begin{matrix} (3.230a) & λ_{S} - λ_{E_{1}} = \tan α_{1} \cdot \ln \tan (45^{\circ} + \frac{φ_{S}}{2}) \cdot \frac{180^{\circ}}{π} (α_{1} \neq 90^{\circ}), \end{matrix}

\begin{matrix} (3.230b) & λ_{S} - λ_{E_{2}} = \tan α_{2} \cdot \ln \tan (45^{\circ} + \frac{φ_{S}}{2}) \cdot \frac{180^{\circ}}{π} (α_{2} \neq 90^{\circ}) . \end{matrix}

消去 $λ_{S}$ 并表示 $φ_{S}$ 给出具有无穷多解的一个方程:

\begin{matrix} (3.231) & φ_{S_{ν}} = 2 \arctan \exp [\frac{λ_{E_{1}} - λ_{E_{2}} + ν \cdot 360^{\circ}}{\tan α_{2} - \tan α_{1}} \cdot \frac{π}{180^{\circ}}] - 90^{\circ} (ν \in Z) . \end{matrix}

相应的地理经度 $λ_{S_{ν}}$ 可以通过在 (3.230a) 中代入 $φ_{S_{ν}}$ 求得

\begin{matrix} (3.232) & λ_{S_{ν}} = λ_{E_{1}} + \tan α_{1} \ln \tan (45^{\circ} + \frac{φ_{S_{ν}}}{2}) \cdot \frac{180^{\circ}}{π} (α_{1} \neq 90^{\circ}) (ν \in Z) . \end{matrix}

评论在某些情形中需要根据 (3.205) 进行角的简化.

3.4.3 球面三角形的计算 ​

3.4.3.1 基本问题、精度评估 ​

3.4.3.2 直角球面三角形 ​

1. 专门公式 ​

2. 纳皮尔法则 ​

3.4.3.3 斜球面三角形 ​

3.4.3.4 球面曲线 ​

1. 大圆航线 ​

2. 小圆 ​

3. 斜航线 ​

4. 球面曲线的交点 ​

3.4.3 球面三角形的计算

3.4.3.1 基本问题、精度评估

3.4.3.2 直角球面三角形

1. 专门公式

2. 纳皮尔法则

3.4.3.3 斜球面三角形

3.4.3.4 球面曲线

1. 大圆航线

2. 小圆

3. 斜航线

4. 球面曲线的交点