18.2.5 无约束问题的解法

考虑一般的优化问题

$$\begin{array}{}\text{(18.72)}& f\left(\underset{―}{\mathbf{x}}\right)=min!,\underset{―}{\mathbf{x}}\in {\mathbb{R}}^n,\end{array}$$

这里 $f$ 是连续可微函数. 本节描述的每一种方法一般是构建一无穷序列 $\left\{{\underset{―}{\mathbf{x}}}^k\right\}\subset {\mathbb{R}}^n$ , 其聚点是一平稳点. 这个点列将从 ${\underset{―}{x}}^1$ 开始,按照如下递推公式构建:

$$\begin{array}{}\text{(18.73)}& {\underset{―}{\mathbf{x}}}^{k+1}={\underset{―}{\mathbf{x}}}^k+{\alpha }_k{\underset{―}{\mathbf{d}}}^k\left(k=1,2,\cdots \right),\end{array}$$

即首先在 ${\underset{―}{x}}^k$ 处确定一方向 ${\underset{―}{d}}^k$ ,而步长 ${\alpha }_k$ 表示在 ${\underset{―}{x}}^k$ 沿 ${\underset{―}{d}}^k$ 方向离 ${\underset{―}{x}}^{k+1}$ 有多远. 这样的方法称作下降法, 是指

$$\begin{array}{}\text{(18.74)}& f\left({\underset{―}{\mathbf{x}}}^{k+1}\right)<f\left({\underset{―}{\mathbf{x}}}^k\right)\left(k=1,2,\cdots \right).\end{array}$$

等式 $\mathrm{\nabla }f\left(\underset{―}{\mathbf{x}}\right)=0$ 刻画平稳点,并且可以用作迭代算法的停止规则,其中 $\mathrm{\nabla }$ 表示梯度算子 (参见第 933 页 13.2.6.1).

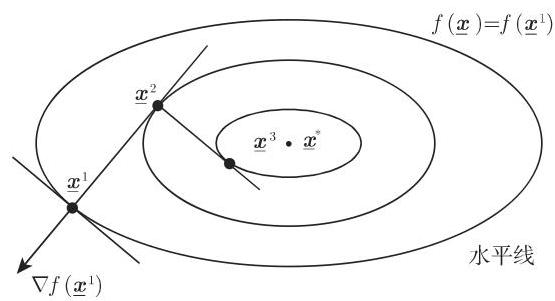
18.2.5.1 最速下降法

从现时点 ${\underset{―}{x}}^k$ 出发,函数下降最快速的方向是

$$\begin{array}{}\text{(18.75a)}& {\underset{―}{\mathbf{d}}}^k=-\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right),\end{array}$$

从而,

$$\begin{array}{}\text{(18.75b)}& {\underset{―}{\mathbf{x}}}^{k+1}={\underset{―}{\mathbf{x}}}^k-{\alpha }_k\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right).\end{array}$$

最速下降法以 $f\left(\underset{―}{\mathbf{x}}\right)=f\left({\underset{―}{\mathbf{x}}}^i\right)$ 为水平线的示意图见图 18.6.

步长 ${\alpha }_k$ 由线搜索确定,即 ${\alpha }_k$ 是一维问题

$$\begin{array}{}\text{(18.76)}& f\left({\underset{―}{\mathbf{x}}}^k+\alpha {\underset{―}{\mathbf{d}}}^k\right)=min!,\alpha \ge 0\end{array}$$

的解. 上述问题可以用 1208 页 18.2.4 给出的方法求解.

最速下降法(18.75b)收敛得相当慢. 对于序列 $\left\{{\underset{―}{x}}^k\right\}$ 的每个聚点 ${\underset{―}{x}}^{\ast }$ ,有 $\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^{\ast }\right)=0$ . 在二次目标函数情形下,即 $f\left(\underset{―}{\mathbf{x}}\right)={\underset{―}{\mathbf{x}}}^{\mathrm{T}}\mathbf{C}\underset{―}{\mathbf{x}}+{\underset{―}{\mathbf{p}}}^{\mathrm{T}}\underset{―}{\mathbf{x}}$ ,该方法取如下特殊形式:

$$\begin{array}{}\text{(18.77a)}& {\underset{―}{\mathbf{x}}}^{k+1}={\underset{―}{\mathbf{x}}}^k+{\alpha }_k{\underset{―}{\mathbf{d}}}^k,\end{array}$$

其中

$$\begin{array}{}\text{(18.77b)}& {\underset{―}{\mathbf{d}}}^k=-\left(2\mathbf{C}{\underset{―}{\mathbf{x}}}^k+\underset{―}{\mathbf{p}}\right),\text{ 且 }{\alpha }_k=\frac{{\underset{―}{\mathbf{d}}}^{k^{\mathrm{T}}}{\mathbf{d}}^k}{2{\underset{―}{\mathbf{d}}}^{k^{\mathrm{T}}}\mathbf{C}{\underset{―}{\mathbf{d}}}^k}.\end{array}$$

18.2.5.2 牛顿法的应用

假定在当前的近似点 ${\underset{―}{x}}^k$ 处,函数 $f$ 由如下二次函数逼近:

$$\begin{array}{}\text{(18.78)}& q\left(\underset{―}{\mathbf{x}}\right)=f\left({\underset{―}{\mathbf{x}}}^k\right)+{(\underset{―}{\mathbf{x}}-{\underset{―}{\mathbf{x}}}^k)}^{\mathrm{T}}\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right)+\frac{1}{2}{(\underset{―}{\mathbf{x}}-{\underset{―}{\mathbf{x}}}^k)}^{\mathrm{T}}\mathbf{H}\left({\underset{―}{\mathbf{x}}}^k\right)\left(\underset{―}{\mathbf{x}}-{\underset{―}{\mathbf{x}}}^k\right).\end{array}$$

这里 $\mathbf{H}\left({\underset{―}{\mathbf{x}}}^k\right)$ 是黑塞矩阵,即 $f$ 在 ${\underset{―}{\mathbf{x}}}^k$ 处的二阶偏导数矩阵. 如果 $\mathbf{H}\left({\underset{―}{\mathbf{x}}}^k\right)$ 是正定的,则 $q\left(\underset{―}{\mathbf{x}}\right)$ 在 ${\underset{―}{\mathbf{x}}}^{k+1}$ 处达到绝对极小,且 $\mathrm{\nabla }q\left({\underset{―}{\mathbf{x}}}^{k+1}\right)=0$ ,从而得到牛顿方法:

$$\begin{array}{}\text{(18.79a)}& {\underset{―}{\mathbf{x}}}^{k+1}={\underset{―}{\mathbf{x}}}^k-{\mathbf{H}}^{-1}\left({\underset{―}{\mathbf{x}}}^k\right)\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right)\left(k=1,2,\cdots \right),\end{array}$$

即

$$\begin{array}{}\text{(18.79b)}& {\underset{―}{\mathbf{d}}}^k=-{\mathbf{H}}^{-1}\left({\underset{―}{\mathbf{x}}}^k\right)\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right),\text{且}{\alpha }_k\text{见 (18.73).}\end{array}$$

牛顿法收敛速度快, 但它也有如下缺点:

a) 矩阵 $\mathbf{H}\left({\underset{―}{\mathbf{x}}}^k\right)$ 必须是正定的.

b) 该方法仅对充分好的初始点收敛.

c) 步长可能没有影响.

d) 该方法并不是一种下降法.

e) 计算逆矩阵 ${\mathbf{H}}^{-1}\left({\underset{―}{\mathbf{x}}}^k\right)$ 的计算量相当大.

通过所谓的阻尼牛顿法可能会适当减少某些缺点 (例如 1251 页 19.2.2.2):

$$\begin{array}{}\text{(18.80)}& {\underset{―}{\mathbf{x}}}^{k+1}={\underset{―}{\mathbf{x}}}^k-{\alpha }_k{\mathbf{H}}^{-1}\left({\underset{―}{\mathbf{x}}}^k\right)\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right)\left(k=1,2,\cdots \right),\end{array}$$

其中的松弛因子 ${\alpha }_k$ 比如可以通过前面给出的原则来确定 (参见第 1210 页 18.2.5.1).

18.2.5.3 共轭梯度法

两个向量 ${\underset{―}{\mathbf{d}}}^1,{\underset{―}{\mathbf{d}}}^2$ 称作相对于对称正定矩阵 $\mathbf{C}$ 是共轭向量,是指它们满足

$$\begin{array}{}\text{(18.81)}& {\underset{―}{\mathbf{d}}}^{1^{\mathrm{T}}}\mathbf{C}{\underset{―}{\mathbf{d}}}^2=0.\end{array}$$

如果 ${\underset{―}{\mathbf{d}}}^1,{\underset{―}{\mathbf{d}}}^2,\cdots ,{\underset{―}{\mathbf{d}}}^n$ 相对于矩阵 $\mathbf{C}$ 是两两共轭的,那么凸二次问题 $q\left(\underset{―}{\mathbf{x}}\right)={\underset{―}{\mathbf{x}}}^{\mathrm{T}}\mathbf{C}\underset{―}{\mathbf{x}}+$ ${\underset{―}{\mathbf{p}}}^{\mathrm{T}}\underset{―}{\mathbf{x}},\underset{―}{\mathbf{x}}\in {\mathbb{R}}^n$ 可以通过 $n$ 步求解,为此只要从 ${\underset{―}{\mathbf{x}}}^1$ 出发构建序列 ${\underset{―}{\mathbf{x}}}^{k+1}={\underset{―}{\mathbf{x}}}^k+{\alpha }_k{\underset{―}{\mathbf{d}}}^k$ , 其中 ${\alpha }_k$ 是最优步长. 假设 $f\left(\underset{―}{x}\right)$ 在 ${\underset{―}{x}}^{\ast }$ 的邻域内是近似二次函数,即 $C\approx \frac{1}{2}H\left({\underset{―}{x}}^{\ast }\right)$ , 则为二次目标函数研发的方法也可应用于更一般的函数 $f\left(\underset{―}{x}\right)$ ,而无须明着使用矩阵 $\mathbf{H}\left({\underset{―}{\mathbf{x}}}^{\ast }\right)$ .

共轭梯度法分如下几个步骤:

**a) ${\underset{―}{x}}^1\ast \ast \in {\mathbb{R}}^n,{\underset{―}{d}}^1=-\mathrm{\nabla }f\left({\underset{―}{x}}^1\right)$ ,其中 ${\underset{―}{x}}^1$ 是 ${\underset{―}{x}}^{\ast }$ 的一个适当的初始近似. (18.82)

**b) ${\underset{―}{\mathbf{x}}}^{k\ast \ast +1}={\underset{―}{\mathbf{x}}}^k+{\alpha }_k{\underset{―}{\mathbf{d}}}^k\left(k=1,\cdots ,n\right)$ ,其中 ${\alpha }_k\ge 0$ 使得 $f\left({\underset{―}{\mathbf{x}}}^k+\alpha {\underset{―}{\mathbf{d}}}^k\right)$ 达到极小.(18.83a)

$$\begin{array}{}\text{(18.83b)}& {\underset{―}{\mathbf{d}}}^{k+1}=-\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^{k+1}\right)+{\mu }_k{\underset{―}{\mathbf{d}}}^k\left(k=1,\cdots ,n-1\right),\end{array}$$

其中

$$\begin{array}{}\text{(18.83c)}& {\mu }_k=\frac{\mathrm{\nabla }f{\left({\underset{―}{\mathbf{x}}}^{k+1}\right)}^{\mathrm{T}}\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^{k+1}\right)}{\mathrm{\nabla }f{\left({\underset{―}{\mathbf{x}}}^k\right)}^{\mathrm{T}}\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right)},{\underset{―}{\mathbf{d}}}^{n+1}=-\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^{n+1}\right).\end{array}$$

c) 用 ${\underset{―}{x}}^{n+1}$ 和 ${\underset{―}{d}}^{n+1}$ 代替 ${\underset{―}{x}}^1$ 和 ${\underset{―}{d}}^1$ ,重复步骤 b).

18.2.5.4 戴维顿 (Davidon)、弗莱彻 (Fletcher) 和鲍威尔 (Powell)(DFP) 方法

在 DFP 方法中,从 ${\underset{―}{x}}^1$ 出发的点列根据下列公式确定:

$$\begin{array}{}\text{(18.84)}& {\underset{―}{\mathbf{x}}}^{k+1}={\underset{―}{\mathbf{x}}}^k-{\alpha }_k{\mathbf{M}}_k\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right)\left(k=1,2,\cdots \right),\end{array}$$

这里 ${\mathbf{M}}_k$ 是对称正定矩阵. 在 $f$ 为二次函数的情形下,这一方法的想法是逆黑塞矩阵由矩阵 ${\mathbf{M}}_k$ 逐步近似. 从对称正定矩阵 ${\mathbf{M}}_1$ ,例如, ${\mathbf{M}}_1=\mathbf{I}(\mathbf{I}$ 为单位矩阵) 出发, ${\mathbf{M}}_k$ 由 ${\mathbf{M}}_{k-1}$ 加上一个 2 秩修正矩阵确定:

$$\begin{array}{}\text{(18.85)}& {\mathbf{M}}_k={\mathbf{M}}_{k-1}+\frac{{\underset{―}{\mathbf{v}}}^k{\underset{―}{\mathbf{v}}}^{k^{\mathrm{T}}}}{{\underset{―}{\mathbf{v}}}^{k^{\mathrm{T}}}{\underset{―}{\mathbf{v}}}^k}-\frac{\left({\mathbf{M}}_{k-1}{\underset{―}{\mathbf{w}}}^k\right){\left({\mathbf{M}}_{k-1}{\underset{―}{\mathbf{w}}}^k\right)}^{\mathrm{T}}}{{\underset{―}{\mathbf{w}}}^{k^{\mathrm{T}}}{\mathbf{M}}_k{\underset{―}{\mathbf{w}}}^k},\end{array}$$

其中 ${\underset{―}{\mathbf{v}}}^k={\underset{―}{\mathbf{x}}}^k-{\underset{―}{\mathbf{x}}}^{k-1},{\underset{―}{\mathbf{w}}}^k=\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right)-\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^{k-1}\right)\left(k=2,3,\cdots \right)$ . 步长 ${\alpha }_k$ 从求解下列优化问题得到:

$$\begin{array}{}\text{(18.86)}& f\left({\underset{―}{\mathbf{x}}}^k-\alpha {\mathbf{M}}_k\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^k\right)\right)=min!,\alpha \ge 0.\end{array}$$

如果 $f\left(\underset{―}{x}\right)$ 是二次函数,则 DFP 方法变成共轭梯度法,相应的初始 ${\mathbf{M}}_1=\mathbf{I}$ .