8.2.1 基本概念、法则和定理

8.2.1.1 定积分的定义与存在性

1. 定积分的定义

有界闭区间 $\left[a,b\right]$ 上的有界函数 $y=f\left(x\right)$ 的定积分是一个数,当 $a<b$ (情形 A) 或 $a>b$ (情形 B) 时,定积分为和的极限. 在后面定积分概念的推广中,也把它看成定义在实直线上任意连通区域, 如开区间或半开区间、半实轴或整个数轴以及分段连通 (除有限个点外处处连通) 区域上的函数, 这类积分属于广义积分 (参见第 673 页 8.2.3).

2. 作为和的极限的定积分

定积分可以定义为如下步骤的极限 (参见第 641 页图 8.1):

第 1 步 在区间 $\left[a,b\right]$ 上任意选取 $n-1$ 个分点 $x_1,x_2,\cdots ,x_{n-1}$ ,且满足下列情形之一:

$$\begin{array}{}\text{(8.37a)}& a=x_0<x_1<x_2<\cdots <x_i<\cdots <x_{n-1}<x_n=b\text{ (情形 A) }\end{array}$$

或

$$\begin{array}{}\text{(8.37b)}& a=x_0>x_1>x_2>\cdots >x_i>\cdots >x_{n-1}>x_n=b\text{ (情形 B),}\end{array}$$

把区间分成 $n$ 个子区间.

第 2 步 如图 8.4 所示,在每个子区间的内部或边界任取一点 ${\xi }_i$ ,使得 $x_{i-1}\le$ ${\xi }_i\le x_i$ (情形 A 中) 或 $x_{i-1}\ge {\xi }_i\ge x_i$ (情形 B 中).(8.37c)

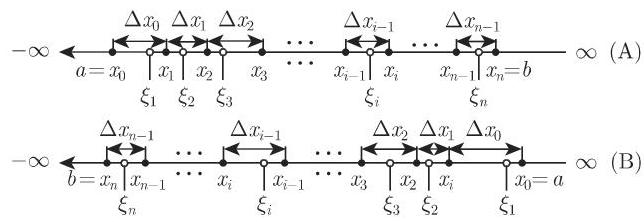
第 3 步 用函数 $f\left(x\right)$ 在所选点处的值 $f\left({\xi }_i\right)$ 乘以子区间的长度,即差 $\mathrm{\Delta }{x}_{i-1}=$ $x_i-x_{i-1}$ ,若为情形 $\mathrm{A}$ ,则差取正号,若为情形 $\mathrm{B}$ ,则差取负号. 情形 $\mathrm{A}$ 中这一步如 641 页图 8.1 所示.

第 4 步 将所有这 $n$ 个乘积 $f\left({\xi }_i\right)\mathrm{\Delta }{x}_{i-1}$ 相加.

第 5 步 当每个子区间的长度都趋于 0,故 $\mathrm{\Delta }{x}_{i-1}$ 也可看作无穷小量,小区间的个数趋于 $\mathrm{\infty }$ 时,计算积分近似和或黎曼和

$$\begin{array}{}\text{(8.38)}& \sum _{i=1}^{n}f\left({\xi }_i\right)\mathrm{\Delta }{x}_{i-1}\end{array}$$

的极限.

若无论 $x_i$ 及 ${\xi }_i$ 的取法如何,极限都存在,则称该极限为函数在所给区间上的定黎曼积分, 记作

$$\begin{array}{}\text{(8.39)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x=\underset{\begin{array}{c}\mathrm{\Delta }{x}_{i-1}\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^{n}f\left({\xi }_i\right)\mathrm{\Delta }{x}_{i-1}.\end{array}$$

称区间的端点为积分限, $a$ 为积分下限, $b$ 为积分上限,区间 $\left[a,b\right]$ 为积分区间, $x$ 为积分变量, $f\left(x\right)$ 为被积函数.

3. 定积分的存在性

闭区间 $\left[a,b\right]$ 上的连续函数定积分存在,即极限 (8.39) 总存在且与 $x_i$ 及 ${\xi }_i$ 的取法无关. 若函数在区间 $\left[a,b\right]$ 有界,且仅有有限个间断点,则其定积分也存在. 在某一给定区间上定积分存在的函数称为该区间上的可积函数.

8.2.1.2 定积分的性质

性质	公式
微积分基本定理 $(f\left(x\right)$ 连续)	${\int }_a^{b}f\left(x\right)\mathrm{d}x={F\left(x\right)|}_a^b=F\left(b\right)-F\left(a\right),$ 其中 $F\left(x\right)=\int f\left(x\right)\mathrm{d}x+C$ 或 $F^{\prime }\left(x\right)=f\left(x\right)$
交换法则	${\int }_a^{b}f\left(x\right)\mathrm{d}x=-{\int }_b^{a}f\left(x\right)\mathrm{d}x$
等积分限	${\int }_a^{a}f\left(x\right)\mathrm{d}x=0$
区间法则	${\int }_a^{b}f\left(x\right)\mathrm{d}x={\int }_a^{c}f\left(x\right)\mathrm{d}x+{\int }_c^{b}f\left(x\right)\mathrm{d}x$
积分变量记号的独立性	${\int }_a^{b}f\left(x\right)\mathrm{d}x={\int }_a^{b}f\left(u\right)\mathrm{d}u={\int }_a^{b}f\left(t\right)\mathrm{d}t$
关于积分上限函数的可微性	$\frac{\mathrm{d}}{\mathrm{d}x}{\int }_a^{x}f\left(t\right)\mathrm{d}t=f\left(x\right)$ ,其中 $f\left(x\right)$ 为连续函数
积分中值定理	${\int }_a^{b}f\left(x\right)\mathrm{d}x=\left(b-a\right)f\left(\xi \right)\left(a<\xi <b\right)$

1. 微积分基本定理

若被积函数 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 连续, $F\left(x\right)$ 为其原函数,则

$$\begin{array}{}\text{(8.40)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x={\int }_a^b{F}^{\prime }\left(x\right)\mathrm{d}x={F\left(x\right)|}_a^b=F\left(b\right)-F\left(a\right),\end{array}$$

即定积分的计算可以化成相应的不定积分的计算, 也就是确定反导数:

$$\begin{array}{}\text{(8.41)}& F\left(x\right)=\int f\left(x\right)\mathrm{d}x+C.\end{array}$$

注 可积函数不一定有原函数, 但连续函数一定有原函数.

2. 几何意义及符号法则

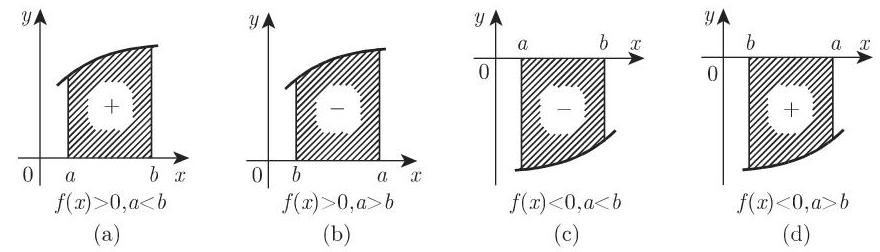
(1) 曲线下的面积 设对 $\mathrm{\forall }x\in \left[a,b\right]$ ,都有 $f\left(x\right)\ge 0$ ,则和 (8.38) 可看作 641 页图 8.1 所有小矩形的总面积,即曲线 $f\left(x\right)$ 下方面积的近似值. 因此和的极限,即函数 $f\left(x\right)$ 的定积分等于曲线 $y=f\left(x\right),x$ 轴以及平行线 $x=a,x=b$ 所围成的区域 $A$ 的面积:

$$\begin{array}{}\text{(8.42)}& A={\int }_a^{b}f\left(x\right)\mathrm{d}x\left(a<b\text{,且当 }a\le x\le b\text{ 时 }f\left(x\right)\ge 0\right).\end{array}$$

(2)符号法则 若函数 $y=f\left(x\right)$ 在积分区间上分段正负 (图 8.5),则相应子区间上的积分, 即各部分面积也有正有负, 故总区间上的积分等于各部分面积的代数和.

图 8.5(a) $\sim$ (d) 给出了面积符号可能出现的四种不同情况.

• $\mathbf{A}:{\int }_0^{\pi }\sin x\mathrm{d}x$ (读作从 $x=0$ 到 $x=\pi$ 上的积分) $=-\cos {x|}_0^{\pi }=\left(-\cos \pi +\cos 0\right)=2$ .

$◼\mathbf{B}$: ${\int }_0^{2\pi }\sin x\mathrm{d}x$ (读作从 $x=0$ 到 $x=2\pi$ 上的积分) $=-\cos x{|}_0^{2\pi }=(-\cos 2\pi +$ $\cos 0)=0$ .

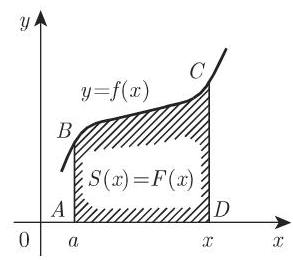
3. 变上限

(1)特别积分 若积分上限为变量 (图 8.6,区域 $ABCD$ ),则存在如下形式的面积函数:

$$\begin{array}{}\text{(8.43)}& S\left(x\right)={\int }_a^{x}f\left(t\right)\mathrm{d}t\left(a<b\text{,且当 }x\ge a\text{ 时 }f\left(x\right)\ge 0\right),\end{array}$$

该积分称为特别积分.

为了避免变上限 $x$ 与积分变量混淆,常常把积分变量记为 $t$ ,如 (8.43) 那样不再使用 $x$ .

(2) 变上限定积分的微分 若变上限定积分 ${\int }_0^{x}f\left(t\right)\mathrm{d}t$ 存在,则它为上限的连续函数 $F\left(x\right)$ . 若 $f\left(x\right)$ 连续,则 $F\left(x\right)$ 关于 $x$ 可微,即 $F\left(x\right)$ 为被积函数的一个原函数. 因此,若 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 上连续,则对任意 $x\in \left(a,b\right)$ ,有

$$\begin{array}{}\text{(8.44)}& F^{\prime }\left(x\right)=f\left(x\right)\text{ 或 }\frac{\mathrm{d}}{\mathrm{d}x}{\int }_a^{x}f\left(t\right)\mathrm{d}t=f\left(x\right).\end{array}$$

该定理的几何意义是变面积 $S\left(x\right)$ 的导数等于线段 $NM$ 的长度 (图 8.7). 正如线段的长度一样, 此处的面积也遵循符号法则 (图 8.5).

4. 积分区间的分解

积分区间 $\left[a,b\right]$ 可以分解成子区间,整个区间上定积分的值

$$\begin{array}{}\text{(8.45)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x={\int }_a^{c}f\left(x\right)\mathrm{d}x+{\int }_c^{b}f\left(x\right)\mathrm{d}x,\end{array}$$

上式称为区间法则. 若被积函数有有限多个跳跃点, 则可将原区间划分成一系列子区间, 使得被积函数在每个子区间上都连续, 于是利用上面的公式, 原积分等于各个子区间上的积分之和.

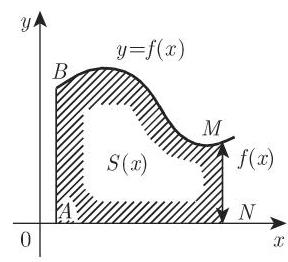
若函数在子区间的端点左极限或右极限存在, 可以以其定义函数的值, 若极限不存在, 则积分为广义积分 (参见第 677 页 8.2.3.3, 1.).

注 若假设等号右侧积分存在,则当 $c$ 位于区间 $\left[a,b\right]$ 的外部时,上述积分公式仍成立.

8.2.1.3 关于积分限的其他定理

1. 积分变量记号的独立性

定积分的值与积分变量的符号无关:

$$\begin{array}{}\text{(8.46)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x={\int }_a^{b}f\left(u\right)\mathrm{d}u={\int }_a^{b}f\left(t\right)\mathrm{d}t.\end{array}$$

2. 等积分限

若积分上限和积分下限相等, 则积分值等于 0 :

$$\begin{array}{}\text{(8.47)}& {\int }_a^{a}f\left(x\right)\mathrm{d}x=0.\end{array}$$

3. 交换积分限

交换积分的上下限后, 积分变号 (交换法则):

$$\begin{array}{}\text{(8.48)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x=-{\int }_b^{a}f\left(x\right)\mathrm{d}x.\end{array}$$

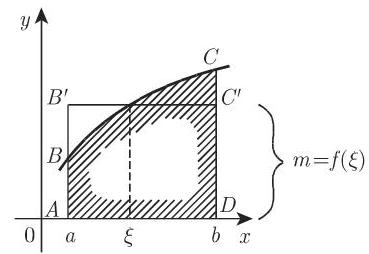
4. 中值定理与中值

(1)中值定理 若函数 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 上连续,则在该区间至少存在一点 $\xi$ ,满足对于情形 $\mathrm{A}$ 中的 $a<\xi <b$ 以及情形 $\mathrm{B}$ 中的 $a>\xi >b$ (参见第 657 页 8.2.1.1,2.), 有

$$\begin{array}{}\text{(8.49)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x=\left(b-a\right)f\left(\xi \right).\end{array}$$

该定理的几何意义为在点 $a,b$ 之间至少存在一点 $\xi$ ,使得图 8.8 中图形 $ABCD$ 的面积等于矩形 $A{B}^{\prime }{C}^{\prime }D$ 的面积.

$$\begin{array}{}\text{(8.50)}& m=\frac{1}{b-a}{\int }_a^{b}f\left(x\right)\mathrm{d}x\end{array}$$

称为区间 $\left[a,b\right]$ 上函数 $f\left(x\right)$ 的中值或算术平均数.

(2) 中值定理的推广 若函数 $f\left(x\right)$ 和 $\phi \left(x\right)$ 均在区间 $\left[a,b\right]$ 上连续,且 $\phi \left(x\right)$ 在该区间不变号,则至少存在一点 $\xi$ ,使得

$$\begin{array}{}\text{(8.51)}& {\int }_a^{b}f\left(x\right)\phi \left(x\right)\mathrm{d}x=f\left(\xi \right){\int }_a^b\phi \left(x\right)\mathrm{d}x\left(a<\xi <b\right).\end{array}$$

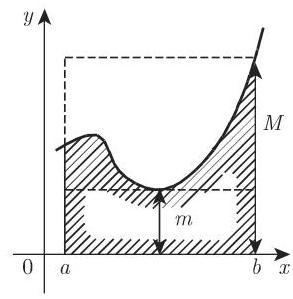
5. 定积分的估计

定积分的值介于区间 $\left[a,b\right]$ 的长度分别与函数在该区间的下确界 $m$ 和上确界 $M$ 的乘积之间:

$$\begin{array}{}\text{(8.52)}& m\left(b-a\right)\le {\int }_a^{b}f\left(x\right)\mathrm{d}x\le M\left(b-a\right)\left(a<b,f\left(x\right)\ge 0\right).\end{array}$$

若函数 $f$ 连续,则 $m$ 为 $f$ 的最小值, $M$ 为 $f$ 的最大值. 由图 8.9,很容易看出该定理的几何意义.

8.2.1.4 定积分的计算

1. 主要方法

计算定积分的主要方法是微积分基本定理, 即转化成不定积分的计算 (参见第 659 页 8.2.1.2,1.), 比如, 可利用 1382 页的表 21.7. 作积分限的代换之前, 要事先检查原积分是否为广义积分.

当今, 常用计算机代数系统可解析地计算不定积分或定积分 (参见第 20 章).

2. 定积分的变换

在很多情况下, 借助代换或分部积分, 作适当变换可计算定积分.

$◼\mathbf{A}$: 对 $I={\int }_0^a\sqrt{a^2-x^2}\mathrm{d}x$ 作代换法.

首先作代换: $x=\phi \left(t\right)=a\sin t$ ,有 $t=\psi \left(x\right)=\arcsin \frac{x}{a},\psi \left(0\right)=0,\psi \left(a\right)=$ $\frac{\pi }{2}$ .

于是

$$I={\int }_0^a\sqrt{a^2-x^2}\mathrm{d}x={\int }_{\arcsin 0}^{\arcsin 1}{a}^2\sqrt{1-{\sin }^{2}t}\cos t\mathrm{d}t$$$$=a^2{\int }_0^{\frac{\pi }{2}}{\cos }^{2}t\mathrm{d}t=a^2{\int }_0^{\frac{\pi }{2}}\frac{1}{2}\left(1+\cos 2t\right)\mathrm{d}t.$$

进一步作代换: $t=\phi \left(z\right)=\frac{z}{2}$ ,有 $z=\psi \left(t\right)=2t,\psi \left(0\right)=0,\psi \left(\frac{\pi }{2}\right)=\pi$ ,于是

$$I={\frac{a^2}{2}t|}_0^{\frac{\pi }{2}}+\frac{a^2}{4}{\int }_0^{\pi }\cos z\mathrm{d}z=\frac{\pi a^2}{4}+{\frac{a^2}{4}\sin z|}_0^{\pi }=\frac{\pi a^2}{4}.$$

$◼\mathbf{B}$: 分部积分法: ${\int }_0^{1}x{\mathrm{e}}^x\mathrm{d}x={\left[x{\mathrm{e}}^x\right]}_0^1-{\int }_0^1{\mathrm{e}}^x\mathrm{d}x=\mathrm{e}-\left(\mathrm{e}-1\right)=1$ .

3. 较难积分的计算方法

若不定积分的计算太过困难与复杂, 或者不能用初等函数来表示, 还可以借助其他方法分几种情况求解定积分的值,比如复变量函数的积分 (参见 $984\sim 989$ 页的例子) 以及含一个参数的积分的微分定理 (参见第 679 页 8.2.4):

$$\begin{array}{}\text{(8.53)}& \frac{\mathrm{d}}{\mathrm{d}t}{\int }_a^{b}f\left(x,t\right)\mathrm{d}x={\int }_a^b\frac{\partial f\left(x,t\right)}{\partial t}\mathrm{d}x.\end{array}$$

$◼I={\int }_0^1\frac{x-1}{\ln x}\mathrm{d}x$ . 引入参数 $t:F\left(t\right)={\int }_0^1\frac{x^t-1}{\ln x}\mathrm{d}x;F\left(0\right)=0;F\left(1\right)=I$ .

对 $F\left(t\right)$ 利用 (8.53),有

$$\frac{\mathrm{d}F}{\mathrm{d}t}={\int }_0^1\frac{\partial }{\partial t}\left[\frac{x^t-1}{\ln x}\right]\mathrm{d}x={\int }_0^1\frac{x^t\ln x}{\ln x}\mathrm{d}x={\int }_0^1{x}^t\mathrm{d}x={\frac{1}{t+1}{x}^{t+1}|}_0^1=\frac{1}{t+1}.$$

积分: $F\left(t\right)-F\left(0\right)={\int }_0^t\frac{\mathrm{d}\tau }{\tau +1}={\ln (\tau +1)|}_0^t=\ln \left(t+1\right)$ ,故 $I=F\left(1\right)=\ln 2$ .

4. 利用级数展开式积分

若被积函数 $f\left(x\right)$ 可展成区间 $\left[a,b\right]$ 上一致收敛的级数

$$\begin{array}{}\text{(8.54)}& f\left(x\right)={\phi }_1\left(x\right)+{\phi }_2\left(x\right)+\cdots +{\phi }_n\left(x\right)+\cdots ,\end{array}$$

则积分可写成如下形式

$$\begin{array}{}\text{(8.55)}& \int f\left(x\right)\mathrm{d}x=\int {\phi }_1\left(x\right)\mathrm{d}x+\int {\phi }_2\left(x\right)\mathrm{d}x+\cdots +\int {\phi }_n\left(x\right)\mathrm{d}x+\cdots \end{array}$$

按此方法可将定积分表示成收敛的数项级数:

$$\begin{array}{}\text{(8.56)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x={\int }_a^b{\phi }_1\left(x\right)\mathrm{d}x+{\int }_a^b{\phi }_2\left(x\right)\mathrm{d}x+\cdots +{\int }_a^b{\phi }_n\left(x\right)\mathrm{d}x+\cdots .\end{array}$$

若函数 ${\phi }_k\left(x\right)$ 易于积分,比如若 $f\left(x\right)$ 能展开成在区间 $\left[a,b\right]$ 上一致收敛的幂级数, 则分 ${\int }_a^{b}f\left(x\right)\mathrm{d}x$ 可以计算到任意精度.

• 计算积分 ${\int }_0^{1/2}{\mathrm{e}}^{-x^2}\mathrm{d}x$ ,将其精确到 0.0001 . 由阿贝尔定理 (参见第 627 页 7.3.3.1),级数 ${\mathrm{e}}^{-x^2}=1-\frac{x^2}{1!}+\frac{x^4}{2!}-\frac{x^6}{3!}+\frac{x^8}{4!}-\cdots$ 在任何有限区间上一致收敛, 因此有 $\int {\mathrm{e}}^{-x^2}\mathrm{d}x=x\left(1-\frac{x^2}{1!\cdot 3}+\frac{x^4}{2!\cdot 5}-\frac{x^6}{3!\cdot 7}+\frac{x^8}{4!\cdot 9}-\cdots \right)$ ,由此得到

$$I={\int }_0^{1/2}{\mathrm{e}}^{-x^2}\mathrm{d}x=\frac{1}{2}\left(1-\frac{1}{2^2\cdot 1!\cdot 3}+\frac{1}{2^4\cdot 2!\cdot 5}-\frac{1}{2^6\cdot 3!\cdot 7}+\frac{1}{2^8\cdot 4!\cdot 9}-\cdots \right)$$$$=\frac{1}{2}\left(1-\frac{1}{12}+\frac{1}{160}-\frac{1}{2688}+\frac{1}{55296}-\cdots \right).$$

为了使积分的计算精度达到 0.0001 , 根据交错级数的莱布尼茨定理 (参见第 621 页 $7.2.3.3,1.)$ ,只需考虑前四项:

$$\$◼\$\approx \frac{1}{2}\left(1-0.08333+0.00625-0.00037\right)$$$$=\frac{1}{2}\cdot 0.92255=0.46127,$$$${\int }_0^{1/2}{\mathrm{e}}^{-x^2}\mathrm{d}x=0.4613$$

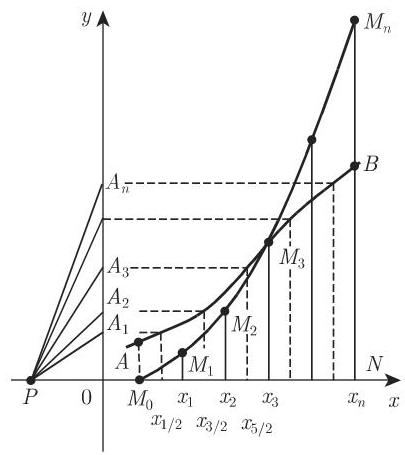
5. 图形积分法

图形积分法是对由曲线 $AB$ 给出的函数 $y=f\left(x\right)$ (图 8.10) 进行积分的图解法,即利用图示计算积分 ${\int }_a^{b}f\left(x\right)\mathrm{d}x$ ,亦即 $M_{0}ABN$ 的面积.

(1) 在区间 $\overline{M_{0}N}$ 插入点 $x_{1/2},x_1,x_{3/2},x_2,\cdots ,x_{n-1},x_{n-1/2}$ ,将其划为 $2n$ 个相等区间, 若插入更多分点, 结果将更精确.

(2) 在点 $x_{1/2},x_{3/2},\cdots ,x_{n-1/2}$ 处作垂线与曲线相交,其交点相应的纵坐标值记为 $\overline{O{A}_1},\overline{O{A}_2},\cdots ,\overline{O{A}_n}$ .

(3) 线段 $\overline{OP}$ 为 $x$ 轴负半轴上的任意长度,将 $P$ 分别连接点 $A_1,A_2,\cdots ,A_n$ .

(4) 过点 $M_0$ 作一条直线与 $P{A}_1$ 平行且与直线 $x=x_1$ 相交,即得线段 $\overline{M_0{M}_1}$ . 过点 $M_1$ 作一条直线与 $P{A}_2$ 平行且与直线 $x=x_2$ 相交,得线段 $\overline{M_1{M}_2}$ ,等等,直到最后到达横坐标为 $x_n$ 的点 $M_n$ .

该积分在数值上等于 $\overline{OP}$ 的长度与 $\overline{N{M}_n}$ 的长度之积:

$$\begin{array}{}\text{(8.57)}& {\int }_a^{b}f\left(x\right)\mathrm{d}x\approx \overline{OP}\cdot \overline{N{M}_n}.\end{array}$$

通过适当地选取任意线段 $\overline{OP}$ ,图示的范围会受到影响; 要想图示越小,需要选取的线段 $\overline{OP}$ 越长. 若 $\overline{OP}=1$ ,则 ${\int }_a^{b}f\left(x\right)\mathrm{d}x=\overline{N{M}_n}$ ,折线 $M_0,M_1,M_2,\cdots ,M_n$ 近似地表示 $f\left(x\right)$ 的一个原函数,即由不定积分 $\int f\left(x\right)\mathrm{d}x$ 给出的一个函数的图像.

6. 面积仪与积分仪

面积仪是测量由封闭平面曲线所围图形面积的工具, 也可用来计算由曲线给定的函数 $y=f\left(x\right)$ 的定积分. 特殊类型的面积仪不仅可以估计 $\int y\mathrm{d}x$ ,还可以估计 $\int y^2\mathrm{d}x$ 和 $\int y^3\mathrm{d}x.$

若函数 $y=f\left(x\right)$ 的图示已知,积分仪是用来绘制它的一个原函数 $Y={\int }_a^{x}f\left(t\right)\mathrm{d}t$ 的工具 (参见 [19.27]).

7. 数值积分

若定积分的被积函数太过复杂, 或其相应的不定积分不能表示成初等函数, 再或仅在一些离散的点处知道函数的值, 比如值表, 则要用到所谓的求积公式或者计算数学中的其他方法 (参见第 1252 页 19.3.1).