10.2.1 等周问题

一般的等周问题(general isoperimetric problem) 是在给定周长的平面区域中确定一个面积最大者. 这个问题的解一具有给定周长的圆, 据传说, 起源于黛多女王 (Queen Dido), 她被允许用一张牛皮所围面积之地建立迦太基 (Carthego) 城. 她把牛皮剪成细条构成一个圆周.

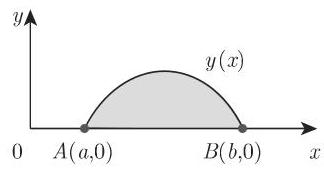
等周问题的一个特殊情形是,在笛卡儿坐标系中求有给定长度 $l$ ,并连接两点 $A\left(a,0\right)$ 和 $B\left(b,0\right)$ 的曲线 $y=y\left(x\right)$ 的方程,使得由直线段 $\overline{AB}$ 和该曲线所围的面积最大 (图 10.1). 从数学形式上来说,要确定一个一次连续可微函数 $y\left(x\right)$ ,使得

$$\begin{array}{}\text{(10.8a)}& I\left[y\right]={\int }_a^{b}y\left(x\right)\mathrm{d}x=max,\end{array}$$$$\begin{array}{}\text{(10.8b)}& G\left[y\right]={\int }_a^b\sqrt{1+y^{\prime 2}\left(x\right)}\mathrm{d}x=l,\end{array}$$$$\begin{array}{}\text{(10.8c)}& y\left(a\right)=y\left(b\right)=0\end{array}$$

成立,其中(10.8b)是附加条件,(10.8c)是边界条件.