Appearance
12.5.6 凸集的分离
1. 超平面
实向量空间
a)
b) 对于任意给定的超子空间
在赋范空间情形,
2. 哈恩-巴拿赫延拓定理的几何形式
设
3. 凸集的分离
实赋范空间
于是若令
在图 12.5(b),(c) 中示出了由超平面分离的两种情形. 为了两个集合的分离, 它们是否相交远非是决定性的因素. 事实上,图 12.5(a) 表示两集
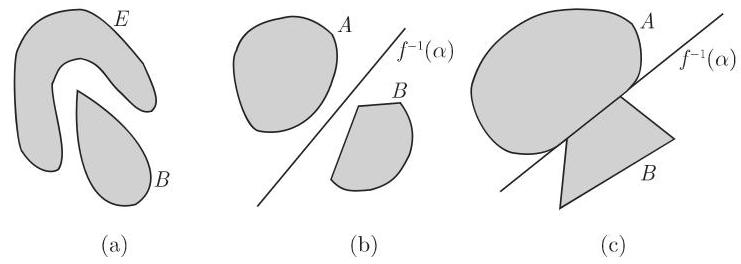
如果
注 著名的库恩-塔克定理 (参见第 1201 页 18.2) 也是基于凸集的分离, 从该定理可导出求解凸优化问题极小值的行之有效的方法.