2.1.4 函数的极限

2.1.4.1 函数极限的定义

若当 $x$ 无限趋近于 $a$ 时,函数 $y=f\left(x\right)$ 无限趋近于 $A$ ,则称 $y=f\left(x\right)$ 在 $x=a$ 处的极限为 $A$ ,记为

$$\begin{array}{}\text{(2.14)}& \underset{x\to a}{lim}f\left(x\right)=A\text{ 或 }f\left(x\right)\to A\left(x\to a\right).\end{array}$$

$f\left(x\right)$ 在 $a$ 点不一定有定义,即便有定义, $f\left(a\right)$ 也未必等于 $A$ .

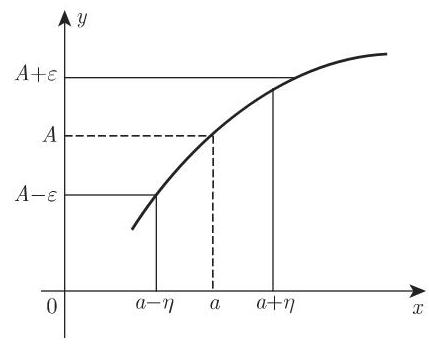
精确定义 若对任意正数 $\epsilon$ ,都存在正数 $\eta$ ,使得对定义域中的每个 $x$ ,当 $x\ne a$ ,且

$$\begin{array}{}\text{(2.15a)}& \left|x-a\right|<\eta \end{array}$$

时, 不等式

$$\begin{array}{}\text{(2.15b)}& \left|f\left(x\right)-A\right|<\epsilon \end{array}$$

恒成立 (图 2.7),则称极限 (2.14) 存在. 若 $a$ 是一个区间的终点,则不等式 $\left|x-a\right|<$ $\eta$ 可以简化成 $a-\eta <x$ 或 $x<a+\eta$ (也可参见第 70 页 2.1.4.5).

2.1.4.2 序列极限的定义

设函数 $f\left(x\right)$ 在 $x=a$ 处的极限为 $A$ ,则对定义域中每个收敛于 $a$ (但不等于 $a$ ) 的 $x$ 的序列 $x_1,x_2,\cdots ,x_n,\cdots$ ,相应的函数值序列 $f\left(x_1\right),f\left(x_2\right),\cdots ,f\left(x_n\right),\cdots$ 收敛于 $A$ (参见第 614 页 7.1.2).

2.1.4.3 柯西收敛准则

函数 $f\left(x\right)$ 在 $x=a$ 处有极限的充分必要条件是: 若 $x_1,x_2$ 为定义域内的任意两个不等于 $a$ 且与 $a$ 足够接近的变量,则 $f\left(x_1\right)$ 与 $f\left(x_2\right)$ 也足够接近.

精确定义 函数 $f\left(x\right)$ 在 $x=a$ 处有极限的充分必要条件是: 若对任意正数 $\epsilon$ ,都存在正数 $\eta$ ,使得对定义域中的任意 $x_1,x_2$ ,当

$$\begin{array}{}\text{(2.16a)}& 0<\left|x_1-a\right|<\eta ,0<\left|x_2-a\right|<\eta \end{array}$$

时, 不等式

$$\begin{array}{}\text{(2.16b)}& \left|f\left(x_1\right)-f\left(x_2\right)\right|<\epsilon \end{array}$$

成立.

2.1.4.4 函数极限为无穷

符号

$$\begin{array}{}\text{(2.17)}& \underset{x\to a}{lim}\left|f\left(x\right)\right|=\mathrm{\infty }\end{array}$$

表示当 $x$ 趋近于 $a$ 时,绝对值 $\left|f\left(x\right)\right|$ 没有上界.

精确定义 若对任意给定的正数 $K$ ,都存在正数 $\eta$ ,使得当 $x\ne a$ 且

$$\begin{array}{}\text{(2.18a)}& a-\eta <x<a+\eta \end{array}$$

时,都有相应的 $\left|f\left(x\right)\right|$ 大于 $K$ :

$$\begin{array}{}\text{(2.18b)}& \left|f\left(x\right)\right|>K,\end{array}$$

则等式 (2.17) 成立.

若当

$$\begin{array}{}\text{(2.18c)}& a-\eta <x<a+\eta \end{array}$$

时,所有的 $f\left(x\right)$ 均为正数,记作

$$\begin{array}{}\text{(2.18d)}& \underset{x\to a}{lim}f\left(x\right)=+\mathrm{\infty }\end{array}$$

若所有的 $f\left(x\right)$ 均为负数,记作

$$\begin{array}{}\text{(2.18e)}& \underset{x\to a}{lim}f\left(x\right)=-\mathrm{\infty }.\end{array}$$

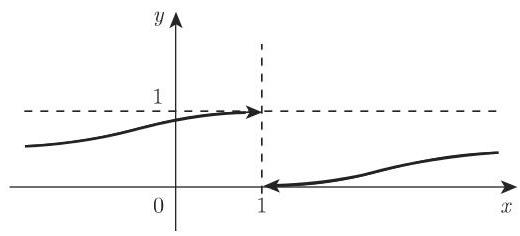
2.1.4.5 函数的左极限和右极限

若 $x$ 从 $a$ 的左侧趋于 $a$ 时,有函数 $f\left(x\right)$ 趋于 $A^{-}$ ,则称 $A^{-}$ 为 $f\left(x\right)$ 在 $x=a$ 处的左极限, 记作

$$\begin{array}{}\text{(2.19a)}& A^{-}=\underset{x\to a-0}{lim}f\left(x\right)=f\left(a-0\right).\end{array}$$

类似地,若 $x$ 从 $a$ 的右侧趋于 $a$ 时,有函数 $f\left(x\right)$ 趋于 $A^{+}$ ,则称 $A^{+}$ 为 $f\left(x\right)$ 在 $x=a$ 处的右极限,记作

$$\begin{array}{}\text{(2.19b)}& A^{+}=\underset{x\to a+0}{lim}f\left(x\right)=f\left(a+0\right).\end{array}$$

仅当左极限与右极限都存在且相等, 即

$$\begin{array}{}\text{(2.19c)}& A^{+}=A^{-}=A\end{array}$$

时,等式 $\underset{x\to a}{lim}f\left(x\right)=A$ 才成立.

$◼$ 当 $x\to 1$ 时,函数 $f\left(x\right)=\frac{1}{1+{\mathrm{e}}^{\frac{1}{x-1}}}$ 的左、右极限不相等: $f\left(1-0\right)=1$ , $f\left(1+0\right)=0\left(\mathrm{图}2.8\right)$ .

2.1.4.6 $x$ 趋于无穷时函数的极限

情形 a) 若对任意正数 $\epsilon$ ,都存在 $N>0$ ,当 $x>N$ 时,有 $A-\epsilon <f\left(x\right)<$ $A+\epsilon$ ,则称数 $A$ 为函数 $f\left(x\right)$ 当 $x\to +\mathrm{\infty }$ 时的极限,记作

$$\begin{array}{}\text{(2.20a)}& \underset{x\to +\mathrm{\infty }}{lim}f\left(x\right)=A.\end{array}$$

类似地,若对任意正数 $\epsilon$ ,都存在 $N>0$ ,当 $x<-N$ 时,有 $A-\epsilon <f\left(x\right)<A+\epsilon$ , 则称数 $A$ 为函数 $f\left(x\right)$ 当 $x\to -\mathrm{\infty }$ 时的极限,记作

$$\begin{array}{}\text{(2.20b)}& \underset{x\to -\mathrm{\infty }}{lim}f\left(x\right)=A.\end{array}$$

$◼\mathbf{A}$: $\underset{x\to +\mathrm{\infty }}{lim}\frac{x+1}{x}=1,$

$◼\mathbf{B}$: $\underset{x\to -\mathrm{\infty }}{lim}\frac{x+1}{x}=1,$

$◼\mathbf{C}$: $\underset{x\to -\mathrm{\infty }}{lim}{\mathrm{e}}^x=0.$

情形 b) 若对任意正数 $K$ ,都存在正数 $N$ ,使得当 $x>N$ 或 $x<-N$ 时,有 $\left|f\left(x\right)\right|>K$ ,则记作

$$\begin{array}{}\text{(2.20c)}& \underset{x\to +\mathrm{\infty }}{lim}\left|f\left(x\right)\right|=\mathrm{\infty }\text{ 或 }\underset{x\to -\mathrm{\infty }}{lim}\left|f\left(x\right)\right|=\mathrm{\infty }.\end{array}$$

$◼\mathbf{A}$: $\underset{x\to +\mathrm{\infty }}{lim}\frac{x^3-1}{x^2}=+\mathrm{\infty },$

$◼\mathbf{B}$: $\underset{x\to -\mathrm{\infty }}{lim}\frac{x^3-1}{x^2}=-\mathrm{\infty },$

$◼\mathbf{C}$: $\underset{x\to +\mathrm{\infty }}{lim}\frac{1-x^3}{x^2}=-\mathrm{\infty },$

$◼\mathbf{D}$: $\underset{x\to -\mathrm{\infty }}{lim}\frac{1-x^3}{x^2}=+\mathrm{\infty }.$

2.1.4.7 函数极限定理

(1)常函数的极限 常函数的极限是这个常数本身:

$$\begin{array}{}\text{(2.21)}& \underset{x\to a}{lim}A=A.\end{array}$$

(2) 和或差的极限 对于有限多个函数, 若每个函数都有极限, 则它们的和或差的极限等于极限的和或差 (若最终表达式不含 $\mathrm{\infty }-\mathrm{\infty }$ 型):

$$\begin{array}{}\text{(2.22)}& \underset{x\to a}{lim}\left[f\left(x\right)+\phi \left(x\right)-\psi \left(x\right)\right]=\underset{x\to a}{lim}f\left(x\right)+\underset{x\to a}{lim}\phi \left(x\right)-\underset{x\to a}{lim}\psi \left(x\right).\end{array}$$

(3) 积的极限 对于有限多个函数, 若每个函数都有极限, 则它们积的极限等于极限的积 (若最终表达式不含 $0\cdot \mathrm{\infty }$ 型):

$$\begin{array}{}\text{(2.23)}& \underset{x\to a}{lim}\left[f\left(x\right)\phi \left(x\right)\psi \left(x\right)\right]=\left[\underset{x\to a}{lim}f\left(x\right)\right]\left[\underset{x\to a}{lim}\phi \left(x\right)\right]\left[\underset{x\to a}{lim}\psi \left(x\right)\right].\end{array}$$

(4) 商的极限 若两个函数的极限都存在且分母极限不等于 0 , 则两函数商的极限等于极限的商 (若最终表达式不是 $\frac{\mathrm{\infty }}{\mathrm{\infty }}$ 型):

$$\begin{array}{}\text{(2.24)}& \underset{x\to a}{lim}\frac{f\left(x\right)}{\phi \left(x\right)}=\frac{\underset{x\to a}{lim}f\left(x\right)}{\underset{x\to a}{lim}\phi \left(x\right)}.\end{array}$$

若分母的极限为 0,通常可以通过检验分子的符号 $\left(\frac{0}{0}\text{型未定式}\right)$ 来判断极限存在与否. 类似地,我们可以通过选取适当的极限的幂来计算幂的极限 (若它不是 $0^0,1^{\mathrm{\infty }}$ 或 ${\mathrm{\infty }}^0$ 型).

(5) 夹逼定理 若函数 $f\left(x\right)$ 的值介于 $\phi \left(x\right)$ 与 $\psi \left(x\right)$ 的值之间,即 $\phi \left(x\right)<$ $f\left(x\right)<\psi \left(x\right)$ ,且 $\underset{x\to a}{lim}\phi \left(x\right)=A,\underset{x\to a}{lim}\psi \left(x\right)=A$ ,则 $f\left(x\right)$ 的极限也存在,且

$$\begin{array}{}\text{(2.25)}& \underset{x\to a}{lim}f\left(x\right)=A.\end{array}$$

2.1.4.8 极限的计算

利用前面五条定理以及一些变形可以计算极限值.

1. 适当的变形

为了计算极限, 需要把表达式变成适当的形式. 不同情况有不同的变形方法, 在此举三个例子.

$◼\mathbf{A}$: $\underset{x\to 1}{lim}\frac{x^3-1}{x-1}=\underset{x\to 1}{lim}\left(x^2+x+1\right)=3$ .

$◼\mathbf{B}$: $\underset{x\to 0}{lim}\frac{\sqrt{1+x}-1}{x}=\underset{x\to 0}{lim}\frac{\left(\sqrt{1+x}-1\right)\left(\sqrt{1+x}+1\right)}{x\left(\sqrt{1+x}+1\right)}=\underset{x\to 0}{lim}\frac{1}{\sqrt{1+x}+1}=\frac{1}{2}$ .

$◼\mathbf{C}$: $\underset{x\to 0}{lim}\frac{\sin 2x}{x}=\underset{x\to 0}{lim}\frac{2\left(\sin 2x\right)}{2x}=2\underset{x\to 0}{lim}\frac{\sin 2x}{2x}=2$ .

2. 伯努利-洛必达 (Bernoulli-l'Hospital) 法则

对于形如 $\frac{0}{0},\frac{\mathrm{\infty }}{\mathrm{\infty }},0\cdot \mathrm{\infty },\mathrm{\infty }-\mathrm{\infty },0^0,{\mathrm{\infty }}^0,1^{\mathrm{\infty }}$ 型的未定式,通常可利用伯努利-洛必达法则(一般简称洛必达法则).

情形 a) $\frac{0}{0}$ 或 $\frac{\mathrm{\infty }}{\mathrm{\infty }}$ 型未定式 利用定理前首先检查 $f\left(x\right)=\frac{\phi \left(x\right)}{\psi \left(x\right)}$ 是否为 $\frac{0}{0}$ 或 $\frac{\mathrm{\infty }}{\mathrm{\infty }}$ 型.

假设 $\phi \left(x\right)$ 和 $\psi \left(x\right)$ 在 $a$ 的某邻域有定义, $\underset{x\to a}{lim}\phi \left(x\right)=0,\underset{x\to a}{lim}\psi \left(x\right)=0$ ,或者 $\underset{x\to a}{lim}\phi \left(x\right)=\mathrm{\infty },\underset{x\to a}{lim}\psi \left(x\right)=\mathrm{\infty }$ ,且二者在 $a$ 的该去心邻域均可导,并有 ${\psi }^{\prime }\left(x\right)\ne 0$ , $\underset{x\to a}{lim}\frac{\phi \left(x\right)}{\psi \left(x\right)}$ 存在,则

$$\begin{array}{}\text{(2.26)}& \underset{x\to a}{lim}f\left(x\right)=\underset{x\to a}{lim}\frac{\phi \left(x\right)}{\psi \left(x\right)}=\underset{x\to a}{lim}\frac{{\phi }^{\prime }\left(x\right)}{{\psi }^{\prime }\left(x\right)}.\end{array}$$

注 若导数比值的极限不存在, 并不意味着原式极限不存在. 可能极限存在, 但是不能通过洛必达法则来判断.

若 $\underset{x\to a}{lim}\frac{{\phi }^{\prime }\left(x\right)}{{\psi }^{\prime }\left(x\right)}$ 仍为未定式,分子和分母满足上述定理的条件,可以再次使用洛必达法则.$\underset{x\to 0}{lim}\frac{\ln \sin 2x}{\ln \sin x}=\underset{x\to 0}{lim}\frac{\frac{2\cos 2x}{\sin 2x}}{\frac{\cos x}{\sin x}}=\underset{x\to 0}{lim}\frac{2\tan x}{\tan 2x}=\underset{x\to 0}{lim}\frac{\frac{2}{{\cos }^{2}x}}{\frac{2}{{\cos }^{2}2x}}=\underset{x\to 0}{lim}\frac{{\cos }^{2}2x}{{\cos }^{2}x}=1.$

情形 b) $0\mathrm{\infty }$ 型未定式 若 $f\left(x\right)=\phi \left(x\right)\psi \left(x\right),\underset{x\to a}{lim}\phi \left(x\right)=0,\underset{x\to a}{lim}\psi \left(x\right)=\mathrm{\infty }$ , 为了对 $\underset{x\to a}{lim}f\left(x\right)$ 应用洛必达法则,要把它变为 $\underset{x\to a}{lim}\frac{\phi \left(x\right)}{\frac{1}{\psi \left(x\right)}}$ 或 $\underset{x\to a}{lim}\frac{\psi \left(x\right)}{\frac{1}{\phi \left(x\right)}}$ 的形式, 由此它化简成了情形 a) 中的 $\frac{0}{0}$ 或 $\frac{\mathrm{\infty }}{\mathrm{\infty }}$ 型未定式.

$◼\underset{x\to \frac{\pi }{2}}{lim}\left(\pi -2x\right)\tan x=\underset{x\to \frac{\pi }{2}}{lim}\frac{\pi -2x}{\cot x}=\underset{x\to \frac{\pi }{2}}{lim}\frac{-2}{-\frac{1}{{\sin }^{2}x}}=2.$

情形 c) $\mathrm{\infty }-\mathrm{\infty }$ 型未定式 若 $f\left(x\right)=\phi \left(x\right)-\psi \left(x\right),\underset{x\to a}{lim}\phi \left(x\right)=\mathrm{\infty },\underset{x\to a}{lim}\psi \left(x\right)=$ $\mathrm{\infty }$ ,则通常可采用几种不同方法把表达式转换成 $\frac{0}{0}$ 或 $\frac{\mathrm{\infty }}{\mathrm{\infty }}$ 型未定式,如 $\phi -\psi =$ $\left(\frac{1}{\psi }-\frac{1}{\phi }\right)/\frac{1}{\phi \psi }$ ,再利用情形 a) 的方法.

• $\underset{x\to 1}{lim}\left(\frac{x}{x-1}-\frac{1}{\ln x}\right)=\underset{x\to 1}{lim}\left(\frac{x\ln x-x+1}{x\ln x-\ln x}\right)=\frac{0}{0}$ ,再利用两次洛必达法则, 得到

$$\underset{x\to 1}{lim}\left(\frac{x\ln x-x+1}{x\ln x-\ln x}\right)=\underset{x\to 1}{lim}\left(\frac{\ln x}{\ln x+1-\frac{1}{x}}\right)=\underset{x\to 1}{lim}\left(\frac{\frac{1}{x}}{\frac{1}{x}+\frac{1}{x^2}}\right)=\frac{1}{2}.$$

情形 d) $0^0,{\mathrm{\infty }}^0,1^{\mathrm{\infty }}$ 型未定式 若 $f\left(x\right)=\phi {\left(x\right)}^{\psi \left(x\right)},\underset{x\to a}{lim}\phi \left(x\right)=+0$ , $\underset{x\to a}{lim}\psi \left(x\right)=0$ ,首先要计算 $\ln f\left(x\right)=\psi \left(x\right)\ln \phi \left(x\right)$ 的极限 $A$ ,变成 $0\cdot \mathrm{\infty }$ 型 (情形 b)),则有 $\underset{x\to a}{lim}f\left(x\right)={\mathrm{e}}^A$ .

类似地,可计算 ${\mathrm{\infty }}^0,1^{\mathrm{\infty }}$ 型未定式.

${lim}_{x\to +0}{x}^x=X,\ln x^x=x\ln x,\underset{x\to +0}{lim}x\ln x=\underset{x\to +0}{lim}\frac{\ln x}{x^{-1}}=\underset{x\to +0}{lim}\left(-x\right)=0$ ,即 $A=\ln X=0$ ,故 $X=1$ ,因此 $\underset{x\to +0}{lim}{x}^x=1$ .

3. 泰勒展开式

对于未定型, 除了利用洛必达法则外, 也可以将表达式展开成泰勒级数 (参见第 594 页 6.1.4.5).

$$◼\underset{x\to 0}{lim}\frac{x-\sin x}{x^3}=\underset{x\to 0}{lim}\frac{x-\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots \right)}{x^3}=\underset{x\to 0}{lim}\left(\frac{1}{3!}-\frac{x^2}{5!}+\cdots \right)=\frac{1}{6}.$$

2.1.4.9 函数的量级与朗道符号

比较两个函数时,常常要考虑它们关于某个自变量 $x=a$ 的相互关系,此外也很容易比较它们的量级.

(1) 若当 $x$ 趋于 $a$ 时, $\left|f\left(x\right)\right|,\left|g\left(x\right)\right|$ 及 $\left|\frac{f\left(x\right)}{g\left(x\right)}\right|$ 均为无穷大,则称在 $a$ 点函数 $f\left(x\right)$ 是比 $g\left(x\right)$ 低阶的 (速度更快) 无穷大.

(2) 若当 $x$ 趋于 $a$ 时, $\left|f\left(x\right)\right|,\left|g\left(x\right)\right|$ 及 $\left|\frac{f\left(x\right)}{g\left(x\right)}\right|$ 均趋于 0,则称在 $a$ 点函数 $f\left(x\right)$ 是比 $g\left(x\right)$ 高阶的无穷小.

(3) 若当 $x$ 趋于 $a$ 时, $0<m<\left|\frac{f\left(x\right)}{g\left(x\right)}\right|<M,m,M$ 为常数,则函数 $f\left(x\right)$ 与 $g\left(x\right)$ 是同阶无穷小或无穷大.

(4) 朗道符号 两个函数在 $x=a$ 的关系可以用朗道符号 $O$ (“大 $\mathrm{O}$ ”) 或 $o$ (“小 o") 来描述,具体如下: 当 $x\to a$ 时,

$$\begin{array}{}\text{(2.27a)}& f\left(x\right)=O\left(g\left(x\right)\right)\text{ 表示 }\underset{x\to a}{lim}\frac{f\left(x\right)}{g\left(x\right)}=A\ne 0,A\text{ 为常数. }\end{array}$$$$\begin{array}{}\text{(2.27b)}& f\left(x\right)=o\left(g\left(x\right)\right)\text{ 表示 }\underset{x\to a}{lim}\frac{f\left(x\right)}{g\left(x\right)}=0,\end{array}$$

其中 $a$ 也可以为 $\pm \mathrm{\infty }$ ,且只有假设 $x$ 趋于给定的 $a$ 时,朗道符号才有意义.

$◼\mathbf{A}$: 当 $x\to 0$ 时, $\sin x=O\left(x\right)$ . 事实上,设 $f\left(x\right)=\sin x,g\left(x\right)=x$ ,则 $\underset{x\to 0}{lim}\frac{\sin x}{x}=1\ne 0$ ,即在 $x=0$ 的邻域中, $\sin x$ 与 $x$ 表现形式类似.

$◼\mathbf{B}$: 设 $f\left(x\right)=1-\cos x,g\left(x\right)=\sin x$ ,则当 $x\to 0$ 时, $f\left(x\right)$ 是比 $g\left(x\right)$ 高阶的无穷小. 事实上, $\underset{x\to 0}{lim}\left|\frac{f\left(x\right)}{g\left(x\right)}\right|=\underset{x\to 0}{lim}\left|\frac{1-\cos x}{\sin x}\right|=0$ ,即 $1-\cos x=o\left(\sin x\right)$ .

$◼\mathbf{C}$: 设 $f\left(x\right)=1-\cos x,g\left(x\right)=x^2$ ,则当 $x\to 0$ 时, $f\left(x\right)$ 是 $g\left(x\right)$ 的同阶无穷小. 事实上, $\underset{x\to 0}{lim}\left|\frac{f\left(x\right)}{g\left(x\right)}\right|=\underset{x\to 0}{lim}\left|\frac{1-\cos x}{x^2}\right|=\frac{1}{2}$ ,即 $1-\cos x=O\left(\sin x\right)$ .

(5) 多项式 多项式在 $\pm \mathrm{\infty }$ 的量级可以用它们的次数表示. 因此函数 $f\left(x\right)=x$ 的阶为 $1,n+1$ 次多项式比 $n$ 次多项式高 1 阶.

(6) 指数函数 当 $x\to \mathrm{\infty }$ 时,指数函数 ${\mathrm{e}}^x$ 比任意多次的幂函数 $x^n(n$ 为一个固定的正数) 趋于无穷的速度都快:

$$\begin{array}{}\text{(2.28a)}& \underset{x\to \mathrm{\infty }}{lim}\left|\frac{{\mathrm{e}}^x}{x^n}\right|=\mathrm{\infty }.\end{array}$$

事实上,利用洛必达法则,对于任意自然数 $n$ ,有

$$\begin{array}{}\text{(2.28b)}& \underset{x\to \mathrm{\infty }}{lim}\frac{{\mathrm{e}}^x}{x^n}=\underset{x\to \mathrm{\infty }}{lim}\frac{{\mathrm{e}}^x}{n{x}^{n-1}}=\cdots =\underset{x\to \mathrm{\infty }}{lim}\frac{{\mathrm{e}}^x}{n!}=\mathrm{\infty }.\end{array}$$

(7) 对数函数 对数函数比任意低次的幂函数 $x^{\alpha }$ ( $\alpha$ 为一个固定的正数) 趋于

无穷的速度都慢:

$$\begin{array}{}\text{(2.29)}& \underset{x\to \mathrm{\infty }}{lim}\left|\frac{\log x}{x^{\alpha }}\right|=0.\end{array}$$

利用洛必达法则可以进行证明.