Appearance
2.7.1 基本概念
2.7.1.1 定义及表示
1. 定义
因为三角函数是从几何角度引入进来的, 所以它们的定义及自变量采用角度或者弧度制 (参见第 170 页 3.1.1.5).
2. 正弦
标准正弦函数
是周期为
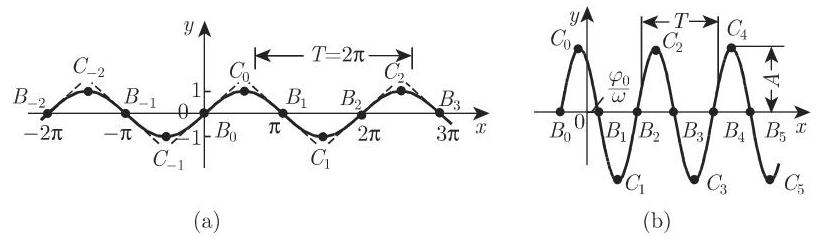
标准正弦曲线与
一般正弦函数
的振幅为
通过比较标准正弦曲线和一般正弦曲线 (图 2.32(b)), 可以看出后者可由前者沿
3. 余弦
标准余弦函数
如图 2.33 所示.
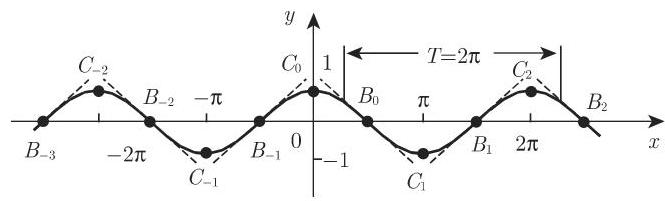
曲线与
一般余弦函数
可以变换成
即由一般正弦函数向左平移
4. 正切
正切函数
的周期
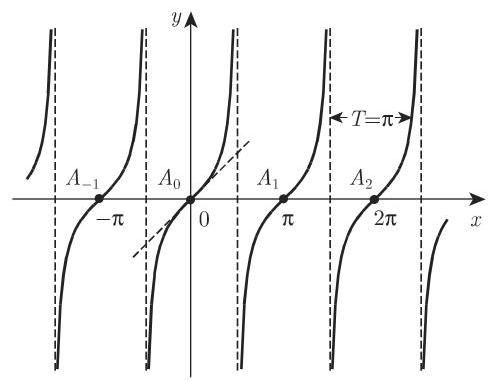
5. 余切
余切函数
的图像可由正切曲线沿
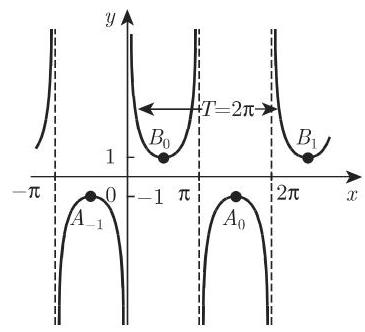
6. 正割
正割函数
的周期
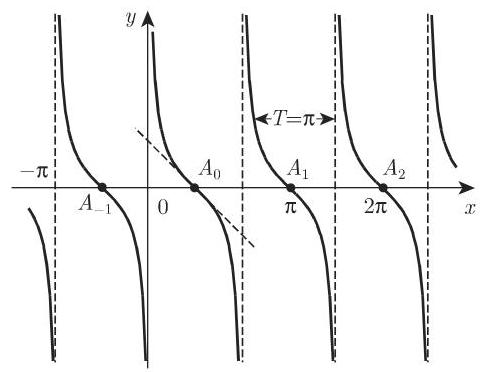
7. 余割
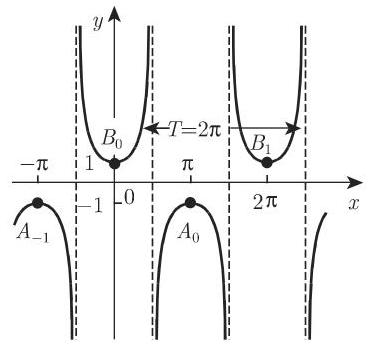
余割函数
的图像可由正割函数图像向右平移
2.7.1.2 函数的值域与性质
1. 角度范围
图 2.38 描述了六个三角函数从
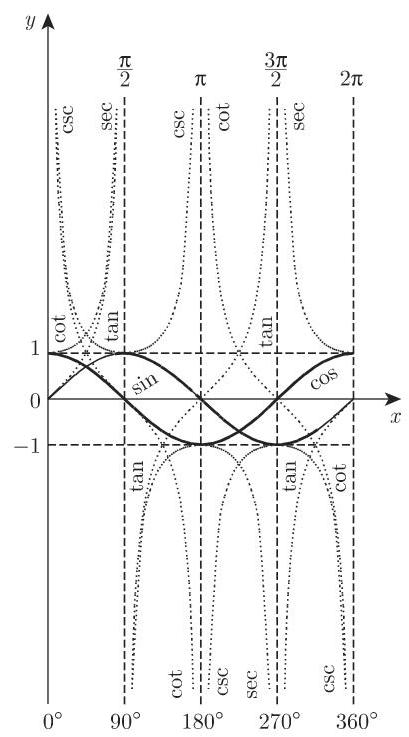
表 2.1 回顾了这些函数的定义域和值域. 函数的符号与自变量所属的象限有关, 见表 2.2 .
定义域 | 值域 | 定义域 | 值域 |
象限 | 角 | sin | COS | tan | cot | sec | CSC |
I | |||||||
II | |||||||
III | |||||||
IV |
2. 某些特殊角的三角函数值 (参见表 2.3)
表
角度 | 弧度 | sin | COS | tan | cot | sec | CSC |
0 | 0 | 1 | 0 | 于 | 1 | 千∞ | |
2 | |||||||
1 | 1 | ||||||
2 | |||||||
1 | 0 | 0 | 1 |
3. 任意角
因为三角函数为周期函数 (周期为
角
角
角
称为余角公式.
函数 | ||||
于 | ||||
∓ cot | ∓ cot | |||
∓ tan | 于 |
若
称为补角公式.
角
4. 弧度角
以弧度制即单位圆弧给出的角, 很容易用公式 (3.2) 进行转换 (参见 170 页3.1.1.5).