5.2.3 关系和映射

1. $n$ 元关系

关系定义一个或不同的集合的元素间的对应. 集合 $A_1,\cdots ,A_n$ 间的 $n$ 元关系或 $n$ 位关系 $R$ 是这些集合的笛卡儿积的子集,即 $R\subseteq A_1\times \cdots \times A_n$ . 如果集合 $A_i\left(i=1,\cdots ,n\right)$ 全是同一个集合 $A$ ,那么有 $R\subseteq A^n$ ,并且将它称作集合 $A$ 中的 $n$ 元关系.

2. 二元关系

(1)集合中二元关系的概念一个集合中二位 (二元) 关系具有特殊的重要性. 在二元关系情形,也经常使用记号 $aRb$ 代替 $\left(a,b\right)\in R$ .

作为一个例子,考虑集合 $A=\{1,2,3,4\}$ 中的整除关系,即二元关系

$$\begin{array}{}\text{(5.67a)}& T=\{\left(a,b\right)\mid a,b\in A\wedge a\text{ 是 }b\text{ 的因子 }\}\end{array}$$$$\begin{array}{}\text{(5.67b)}& =\{\left(1,1\right),\left(1,2\right),\left(1,3\right),\left(1,4\right),\left(2,2\right),\left(2,4\right),\left(3,3\right),\left(4,4\right)\}.\end{array}$$

(2) 箭头图或映射函数 集合 $A$ 中的有限二元关系可以用箭头函数或箭头图或用关系矩阵表示. $A$ 的元素用平面上的点表示,并且若存在关系 $aRb$ ,则表示为一个从 $a$ 到 $b$ 的箭头.

图 5.7 给出 $A=\{1,2,3,4\}$ 中关系 $T$ 的箭头图.

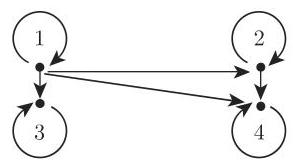
(3) 关系矩阵 $A$ 的元素作为矩阵的行元素和列元素 (参见第 361 页 4.1.1,1.). 若 $aRb$ ,则在 $a\in A$ 所在的行与 $b\in B$ 所在的列的交点处元素为 1,不然为 0 . 下面的表格给出 $A=\{1,2,3,4\}$ 中关系 $T$ 的关系矩阵.

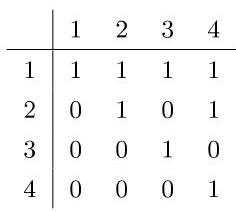
表格: 关系矩阵

3. 关系积、逆关系

关系是特殊的集合, 所以通常的集合运算 (参见第 440 页 5.2.2) 可以在关系间实施. 除此之外, 对于二元关系, 还有关系积和逆关系, 具有特殊重要性.

设 $R\subseteq A\times B$ 和 $S\subseteq B\times C$ 是两个二元关系. 关系 $R,S$ 的积 $R\circ S$ 定义为

$$\begin{array}{}\text{(5.68)}& R\circ S=\{\left(a,c\right)\mid \mathrm{\exists }b\left(b\in B\wedge aRb\wedge bSc\right)\}.\end{array}$$

关系积是结合的, 但不交换.

关系 $R$ 的逆 $R^{-1}$ 定义为

$$\begin{array}{}\text{(5.69)}& R^{-1}=\{\left(b,a\right)\mid \left(a,b\right)\in R\}.\end{array}$$

对于集合 $A$ 中的二元关系,下列关系式成立:

$$\begin{array}{}\text{(5.70a)}& \left(R\cup S\right)\circ T=\left(R\circ T\right)\cup \left(S\circ T\right),\end{array}$$$$\begin{array}{}\text{(5.70b)}& \left(R\cap S\right)\circ T\subseteq \left(R\circ T\right)\cap \left(S\circ T\right),\end{array}$$$$\begin{array}{}\text{(5.70c)}& {(R\cup S)}^{-1}=R^{-1}\cup S^{-1},\end{array}$$$$\begin{array}{}\text{(5.70d)}& {(R\cap S)}^{-1}=R^{-1}\cap S^{-1},\end{array}$$$$\begin{array}{}\text{(5.70e)}& {(R\circ S)}^{-1}=S^{-1}\circ R^{-1}.\end{array}$$

4. 二元关系的性质

集合 $A$ 中的二元关系可以具有下列特殊的重要性质: $R$ 称为

自反的,如果 $\mathrm{\forall }a\in A$ aRa;(5.71a)

非自反的,如果 $\mathrm{\forall }a\in A\mathrm{\neg }aRa$ ;(5.71b)

对称的,如果 $\mathrm{\forall }a,b\in A\left(aRb\Rightarrow bRa\right)$ ;(5.71c)

反对称的,如果 $\mathrm{\forall }a,b\in A\left(aRb\wedge bRa\Rightarrow a=b\right)$ ;(5.71d)

传递的,如果 $\mathrm{\forall }a,b,c\in A\left(aRb\wedge bRc\Rightarrow aRc\right)$ ;(5.71e)

线性的,如果 $\mathrm{\forall }a,b\in A\left(aRb\vee bRa\right)$ .(5.71f)

这些关系式还可以用关系积刻画. 例如,如果 $R\circ R\subseteq R$ ,则二元关系 $R$ 是传递的. 特别有趣的是,关系 $R$ 的闭包 $\mathrm{tra}\left(R\right)$ . 它是最小的含有 $R$ 的传递关系 (对于子集关系而言). 实际上,

$$\begin{array}{}\text{(5.72)}& \mathrm{tra}\left(R\right)=\bigcup _{n\ge 1}{R}^n=R^1\cup R^2\cup R^3\cup \cdots ,\end{array}$$

其中 $R^n$ 是 $R$ 与自身的 $n$ 次关系积.

设集合 $\{1,2,3,4,5\}$ 上的二元关系 $R$ 由它的关系矩阵 $M$ 给定: 用矩阵乘法计算 $M^2$ ,在此将值 0 和 1 看作真值,并且代替乘法和加法实施逻辑运算合取和析取,那么 $M^2$ 是属于 $R^2$ 的关系矩阵. $R^3,R^4$ 等的关系矩阵可以类似地计算.

$M$	1	2	3	4	5	$M^2$	1	2	3	4	5	$M^3$	1	2	3	4	5
1	1	0	0	1	0	1	1	1	0	1	1	1	1	1	0	1	1
2	0	0	0	1	0	2	0	1	0	0	1	2	0	1	0	1	0
3	0	0	1	0	1	3	0	1	1	0	1	3	0	1	1	1	1
4	0	1	0	0	1	4	0	1	0	1	0	4	0	1	0	1	1
5	0	1	0	0	0	5	0	0	0	1	0	5	0	1	0	0	1

$R\cup R^2\cup R^3$ 的关系矩阵 (即下面的矩阵) 可以用计算矩阵 $M,M^2$ 和 $M^3$ 的析取元素的方式得到. 因为 $M$ 的较高次幂不含有新的元素 1,所以这个矩阵已经与 $\mathrm{tra}\left(R\right)$ 的关系矩阵相同.

$M^2$V $M^3$	1	2	3	4	5
1	1	1	0	1	1
2	0	1	0	1	1
3	0	1	1	1	1
4	0	1	0	1	1
5	0	1	0	1	1

关系矩阵和关系积在图论中路径长度的搜索中有重要应用 (参见第 540 页5.8.2.1).

在有限二元关系情形, 我们可以容易地从箭头图或关系矩阵识别出上面的性质. 例如, 可以从箭头图中的 “自循环圈” 以及关系矩阵中的主对角元 1 看出自反性. 如果每个箭头都伴随一个反方向的箭头, 或者如果关系矩阵是对称矩阵 (参见第 444 页 5.2.3, 2.), 那么箭头图中对称性是显然的. 从箭头图或从关系矩阵还容易看出可除性 $T$ 是自反的但不是对称关系.

5. 映射

从集合 $A$ 到集合 $B$ 的映射或函数(参见第 61 页 2.1.1.1),记作 $f:A\to B$ ,是一个法则,它对于每个元素 $a\in A$ 恰指派一个元素 $b\in B$ ,并称之为 $f\left(a\right)$ . 映射 $f$ 可以看作 $A\times B$ 的一个子集,因而看作一个二元关系:

$$\begin{array}{}\text{(5.73)}& f=\{\left(a,f\left(a\right)\right)\mid a\in A\}\subseteq A\times B.\end{array}$$

a) 如果对于每个 $b\in B$ 至多存在一个 $a\in A$ 使得 $f\left(a\right)=b$ ,那么称 $f$ 是单射 或一对一映射.

b) 如果对于每个 $b\in B$ 至少存在一个 $a\in A$ 使得 $f\left(a\right)=b$ ,那么称 $f$ 是从 $A$ 到 $B$ 的满射.

c) 如果 $f$ 既是单射也是满射,那么 $f$ 称为双射.

如果 $A$ 和 $B$ 是有限集,并且它们之间存在双射,那么 $A$ 和 $B$ 的元素个数相同 (还可参见第 449 页 5.2.5).

对于双射映射 $f:A\to B$ 存在逆关系: $f^{-1}:B\to A$ 称为 $f$ 的逆映射.

映射的关系积用于一个接着一个映射的复合: 如果 $f:A\to B$ 以及 $g:B\to A$ 是映射,那么 $f\circ g$ 也是一个从 $A$ 到 $C$ 的映射,并且定义为

$$\begin{array}{}\text{(5.74)}& \left(f\circ g\right)=g\left(f\left(a\right)\right).\end{array}$$

注 注意这个方程中 $f$ 和 $g$ 的顺序 (在文献中它有不同的处理!).