Appearance
5.8.1 基本概念和记号
1. 无向图和有向图
图
在图的表示中, 用点记图的顶点, 用箭记有向边, 并用没有方向的线记无向边.
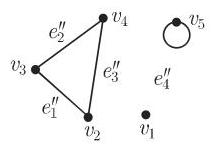
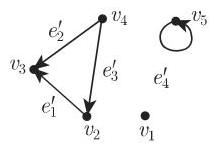
:对于图 5.26 中的图 :
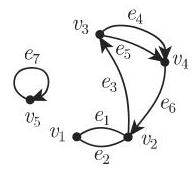
2. 邻接性
如果
无向图中邻接性及无向边的端点可以类似地定义.
3. 简单图
如果多个边或弧指派给同一个顶点的有向对或无向对, 那么它们称为重边. 具有相同的端点边称为环. 没有环和重边及重弧的图称为简单图.
4. 顶点的次数
与一个顶点
对于有向图
5. 特殊的图类
有限图有有限的顶点集和有限的边集. 不然称图是无限的. 在
对于顶点集为
如果一个无向简单图
6. 图的表示
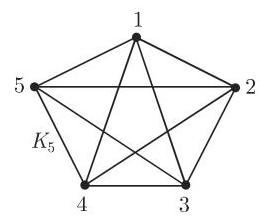
有限图可以直观表示: 对于每个顶点指定平面上一个点, 并且用有向或无向曲线连接两个点 (如果图中有相应的边). 图 5.30 的出一些例子. 图 5.33 给出一些例子. 图 5.33 给出彼得森 (Petersen) 图, 它是几个还没有一般性地证明的图论猜想中的一个著名的反例.
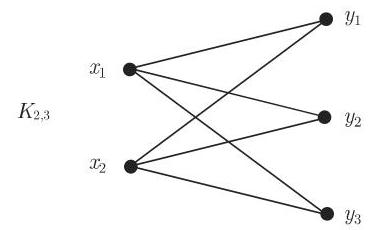
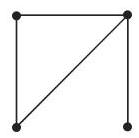
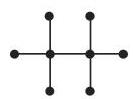

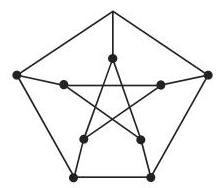
7. 图的同构
图
8. 子图、因子
如果
使得
图
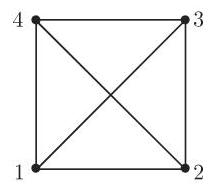
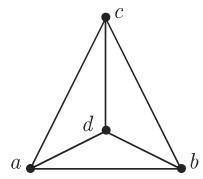
9. 邻接矩阵
有限图可以用矩阵刻画: 设
即当且仅当存在一条从
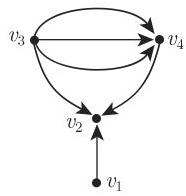
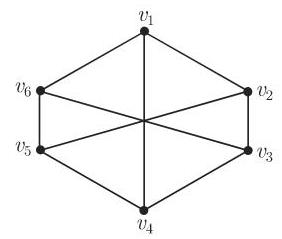
10. 关联矩阵
对于无向图
给出的(n, m)型矩阵
对于有向图
定义的(n, m)型矩阵.
11. 加权图
如果
在应用中, 这些边的权表示由构建、维护或通信产生的费用.