3.3.2 棱角、隅角、立体角

(1)棱角或二面角是从同一条直线出发的两个半平面形成的图形 (图 3.49). 在日常用语中,棱这个字是指两个半平面的交线. 我们用平面棱角 $ABC$ 来度量二面角,它是位于两个半平面并在点 $B$ 与交线 $DE$ 垂直的两条半直线之间的夹角.

(2) 隅角或多面角 $OABCDE$ (图 3.50) 是由若干平面,即侧面形成的图形,它们过一个公共点,即顶点 $O$ ,并分别交于直线 $OA,OB,\cdots$ .

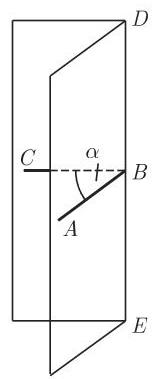
界定同一侧面的两条直线形成一个平面角, 而相邻的面则形成一个二面角.

如果两个多面体可以重叠, 则它们彼此相等, 即它们是全等的. 此时对应的元素, 即棱和顶点处的平面角一定重合. 如果两个多面体在顶点处对应的元素相等, 但它们具有相反的顺序, 则两个隅角不能重叠, 此时称它们为对称隅角, 因为如图 3.51 显示的那样, 可以将它们放在彼此对称的位置.

凸多面角完全位于它的每个面的一侧.

对每个凸多面体来说,平面角之和 $AOB+BOC+\cdots +EOA$ (图 3.50) 小于 ${360}^{\circ }$ .

(3) 两个三面角如果有下列元素重合就是全等的:

• 两个面和对应的二面角,

-个面和属于它的两个二面角,

• 按相同顺序排列的三个对应的面,

• 按相同顺序排列的三个对应的二面角.

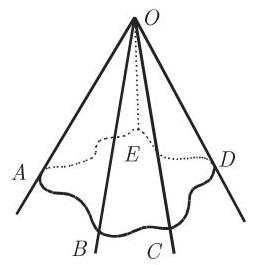
(4)立体角 从同一点出发 (并与一条封闭曲线相截) 的一束射线形成空间中的一个立体角 (图 3.52). 它被记作 $\mathrm{\Omega }$ 并由等式

$$\begin{array}{}\text{(3.115a)}& \mathrm{\Omega }=\frac{S}{r^2}\end{array}$$

计算,这里 $S$ 是指由立体角从一个半径为 $r$ ,中心位于该立体角顶点的球切下来的一片球面. 立体角的单位是球面度(sr):

$$\begin{array}{}\text{(3.115b)}& 1\mathrm{sr}=\frac{1{\mathrm{m}}^2}{1{\mathrm{m}}^2},\end{array}$$

即一个 $1\mathrm{sr}$ 的立体角从单位球 $\left(r=1\mathrm{m}\right)$ 切下来 $1{\mathrm{m}}^2$ 面积的球面.

$◼\mathbf{A}$: 全立体角是 $\mathrm{\Omega }=4\pi r^2/r^2=4\pi$ .

$◼\mathbf{B}$: 一个具有顶角 $\alpha ={120}^{\circ }$ 的锥面定义 (确定) 了一个立体角

$$\mathrm{\Omega }=2\pi r^2\frac{1-\cos \frac{\alpha }{2}}{r^2}=\pi ,$$

其中用到了球冠 (3.163) 的公式.