6.1.4 微分学基本定理

6.1.4.1 单调性

若函数 $f\left(x\right)$ 在一连通区间上有定义且连续,并对该区间的每个内点都可微,则

$f\left(x\right)$ 为单调递增函数,当且仅当 $f^{\prime }\left(x\right)\ge 0$ ;(6.26a)

$f\left(x\right)$ 为单调递减函数,当且仅当 $f^{\prime }\left(x\right)\le 0$ .(6.26b)

若函数严格单调递增或递减,则在给定区间的任意子区间上导函数 $f^{\prime }\left(x\right)$ 不恒等于 0 . 例如,图 6.6(b) 上的线段 $\overline{BC}$ 不满足该条件.

单调性的几何意义为: 单调递增函数的曲线不会随着自变量的增加而下降, 即或者上升或者沿水平方向移动 (图 6.6(a)),因此曲线任意一点的切线或者与 $x$ 轴正半轴的夹角为锐角,或者与 $x$ 轴平行; 当函数单调递减时 (图 6.6(b)),叙述与递增时类似. 若函数严格单调,则具有平行于 $x$ 轴的切线仅在某些点取得,例如图 6.6(a) 中的点 $A$ ,也就是不可能在图 6.6(b) 那样的子区间 $\overline{BC}$ 取得.

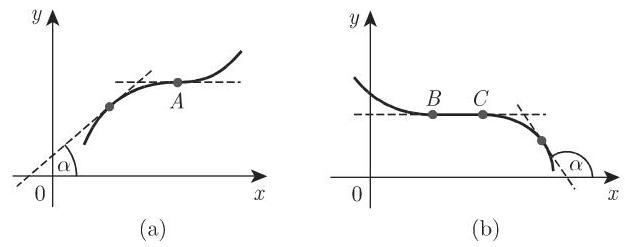
6.1.4.2 费马定理

若函数 $y=f\left(x\right)$ 在一连通区间上有定义,在该区间的内点 $x=c$ 处有极大值或极小值,即对该区间的任一点 $x$ ,有

$$\begin{array}{}\text{(6.27a)}& f\left(c\right)>f\left(x\right)\end{array}$$

或

$$\begin{array}{}\text{(6.27b)}& f\left(c\right)<f\left(x\right),\end{array}$$

且函数在点 $c$ 可导,则在点 $c$ 导数一定等于 0 :

$$\begin{array}{}\text{(6.27c)}& f^{\prime }\left(c\right)=0.\end{array}$$

费马定理的几何意义: 若函数满足定理假设条件,则曲线在点 $A$ 和 $B$ 具有平行于 $x$ 轴的切线 (图 6.7).

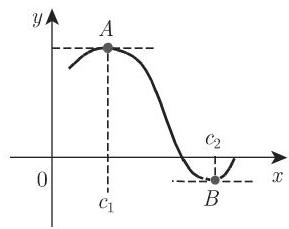
费马定理仅为函数在一点取得极大值和极小值的必要条件. 由图 6.6(a), 显然导数等于 0 不是函数取得极值的充分条件: 在点 $A,f^{\prime }\left(x\right)=0$ ,但在此处无极大值或极小值.

同样,可微也不是取得极值的必要条件. 例如图 6.8(d) 在 $e$ 点具有极大值,但是该点导数不存在.

6.1.4.3 罗尔定理

若函数 $y=f\left(x\right)$ 在闭区间 $\left[a,b\right]$ 连续,开区间(a, b)可微,且

$$\begin{array}{}\text{(6.28a)}& f\left(a\right)=0,f\left(b\right)=0\left(a<b\right),\end{array}$$

则 $a,b$ 间至少存在一点 $c$ ,使得

$$\begin{array}{}\text{(6.28b)}& f^{\prime }\left(c\right)=0\left(a<c<b\right).\end{array}$$

罗尔定理的几何意义: 若区间(a, b)上连续函数 $y=f\left(x\right)$ 的图像与 $x$ 轴交于 $A,B$ 两点,且在每一点都没有垂直切线,则 $A,B$ 间至少存在一点 $C$ ,使得该点处的切线与 $x$ 轴平行 (图 6.8(a)). 在此区间可能有多个这样的点,如图 6.8(b) 中的点 $C,D,E$ . 定理中连续性和可微性的性质非常重要: 图 6.8(c) 中的函数在 $x=d$ 处不连续,图 6.8(d) 中的函数在 $x=e$ 处不可微,在这两种情况下,对于任意导数存在的点,都有 $f^{\prime }\left(x\right)\ne 0$ .

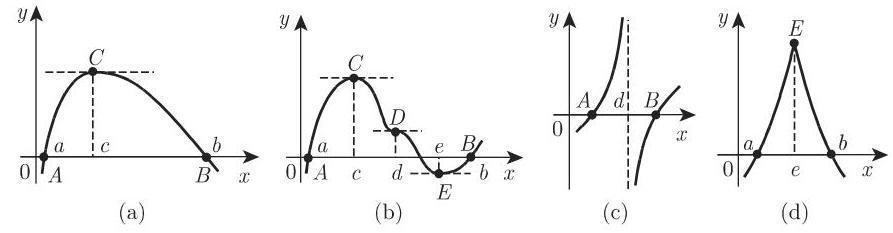
6.1.4.4 微分中值定理

若函数 $y=f\left(x\right)$ 在闭区间 $\left[a,b\right]$ 连续,开区间(a, b)可微,则在 $a,b$ 间至少存在一点 $c$ ,满足

$$\begin{array}{}\text{(6.29a)}& \frac{f\left(b\right)-f\left(a\right)}{b-a}=f^{\prime }\left(c\right)\left(a<c<b\right).\end{array}$$

令 $b=a+h,\theta$ 为介于 0 和 1 之间的一个数,则该定理可写为如下形式:

$$\begin{array}{}\text{(6.29b)}& f\left(a+h\right)=f\left(a\right)+h{f}^{\prime }\left(a+\mathrm{\Theta }h\right)\left(0<\mathrm{\Theta }<1\right).\end{array}$$

(1) 几何意义 定理的几何意义: 若函数 $y=f\left(x\right)$ 满足定理条件,则函数图像在 $A,B$ 间至少有一点 $C$ ,使得该点处的切线与线段 $AB$ 平行 (图 6.9). 也可能存在多个这样的点 (图 6.8(b)).

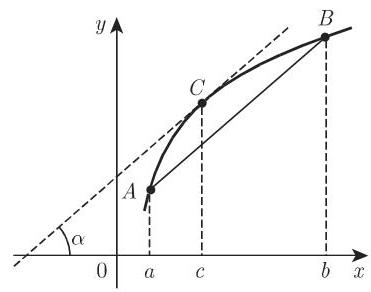
通过例子以及图 6.8(c), (d) 可以看出, 连续性与可微性的性质非常重要. (2)应用 中值定理有几种重要应用.

$◼\mathbf{A}$: 该定理可以证明如下形式的不等式:

$$\begin{array}{}\text{(6.30)}& \left|f\left(b\right)-f\left(a\right)\right|<K\left|b-a\right|,\end{array}$$

对区间 $\left[a,b\right]$ 内的每一点, $K$ 为 $\left|f^{\prime }\left(x\right)\right|$ 的上界.

$◼\mathbf{B}$: 若用 $\pi$ 的近似值 $\overline{\pi }=3.14$ 代替 $\pi ,f\left(\pi \right)=\frac{1}{1+{\pi }^2}$ 的精度如何?

我们有: $\left|f\left(\pi \right)-f\left(\overline{\pi }\right)\right|=\left|\frac{2c}{{(1+c^2)}^2}\right|\left|\pi -\overline{\pi }\right|\le 0.053\cdot 0.0016=0.000085$ ,意即 $\frac{1}{1+{\pi }^2}$ 处于 $0.092084-0.000085$ 与 $0.092084+0.000085$ 之间.

6.1.4.5 一元函数的泰勒定理

若函数 $y=f\left(x\right)$ 在区间 $\left[a,a+h\right]$ 上 $n-1$ 次连续可微 (具有连续导数),且在区间内部也存在 $n$ 阶导数,则泰勒公式或泰勒展开式为

$$f\left(a+h\right)=f\left(a\right)+\frac{h}{1!}{f}^{\prime }\left(a\right)+\frac{h^2}{2!}{f}^{\prime \prime }\left(a\right)+\cdots +\frac{h^{n-1}}{\left(n-1\right)!}{f}^{(n-1)}\left(a\right)+\frac{h^n}{n!}{f}^{\left(n\right)}\left(a+\mathrm{\Theta }h\right),$$

(6.31)

其中 $0<\mathrm{\Theta }<1,h$ 可正可负. 中值定理 (6.29b) 是泰勒公式在 $n=1$ 时的特例.

6.1.4.6 广义微分中值定理 (柯西定理)

若两函数 $y=f\left(x\right)$ 和 $y=\phi \left(x\right)$ 在闭区间 $\left[a,b\right]$ 连续,至少在区间内部可微, 且在该区间上 ${\phi }^{\prime }\left(x\right)\ne 0$ ,则 $a,b$ 间至少存在一点 $c$ ,使得

$$\begin{array}{}\text{(6.32)}& \frac{f\left(b\right)-f\left(a\right)}{\phi \left(b\right)-\phi \left(a\right)}=\frac{f^{\prime }\left(c\right)}{{\phi }^{\prime }\left(c\right)}\left(a<c<b\right).\end{array}$$

广义中值定理的几何意义与第一个中值定理的几何意义相对应. 例如, 设图 6.9 中曲线的参数方程为 $x=\phi \left(t\right),y=f\left(t\right)$ ,则点 $A,B$ 分别对应参数 $t=a,t=b$ 的函数值,因此在点 $C$ ,

$$\begin{array}{}\text{(6.33)}& \tan \alpha =\frac{f\left(b\right)-f\left(a\right)}{\phi \left(b\right)-\phi \left(a\right)}=\frac{f^{\prime }\left(c\right)}{{\phi }^{\prime }\left(c\right)}.\end{array}$$

当 $\phi \left(x\right)=x$ 时,广义中值定理简化成了第一个中值定理.