3.2.1 三角形

3.2.1.1 平面直角三角形中的计算

1. 基本公式

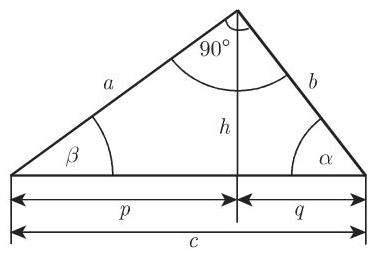
记号 (图 3.31):

$c$ 为斜边; $a,b$ 为其他两边,或两直角边; $\alpha$ 和 $\beta$ 为边 $a$ 和 $b$ 分别所对应的角; $h$ 为高; $p,q$ 为斜边上的线段; $S$ 为面积.

内角之和

$$\begin{array}{}\text{(3.83)}& \alpha +\beta +\gamma ={180}^{\circ },\gamma ={90}^{\circ },\end{array}$$

边的计算

$$a=c\sin \alpha =c\cos \beta$$$$\begin{array}{}\text{(3.84)}& =b\tan \alpha =b\cot \beta ,\end{array}$$

毕达哥拉斯 (勾股) 定理

$$\begin{array}{}\text{(3.85)}& a^2+b^2=c^2.\end{array}$$

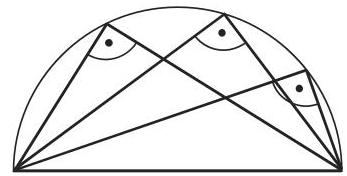
泰勒斯定理 半圆中以直径为底的所有内接三角形的顶角是直角, 即半圆中直径上的所有圆周角是直角 (参见图 3.32 和第 185 页 (3.65b)).

欧几里得定理

$$\begin{array}{}\text{(3.86)}& h^2=pq,a^2=pc,b^2=qc.\end{array}$$

面积

$$\begin{array}{}\text{(3.87)}& S=\frac{ab}{2}=\frac{a^2}{2}\tan \beta =\frac{c^2}{4}\sin 2\beta .\end{array}$$

2. 平面直角三角形边和角的计算

在一个直角三角形中有六个定义量 (三个角 $\alpha ,\beta ,\gamma$ 和它们所对的边 $a,b,c$ ,当然,它们不全都独立),一个角 (图 3.31 中的角 $\gamma$ ) 已知为 ${90}^{\circ }$ .

一个平面三角形可以由三个定义量确定, 但它们不能任意给定 (参见第 173 页 3.1.3.1). 因此在直角三角形的情形中, 只能再给定两个量. 剩下的三个量可以由表 3.3 以及 (3.15) 和 (3.83) 确定.

已知	其他量的计算
例如 $a,\alpha$	$\beta ={90}^{\circ }-\alpha$	$b=a\cot \alpha$	$c=\frac{a}{\sin \alpha }$
例如 $b,\alpha$	$\beta ={90}^{\circ }-\alpha$	$a=b\tan \alpha$	$c=\frac{b}{\cos \alpha }$
例如 $c,\alpha$	$\beta ={90}^{\circ }-\alpha$	$a=c\sin \alpha$	$b=c\cos \alpha$
例如 $a,b$	$\frac{a}{b}=\tan \alpha$	$c=\frac{a}{\sin \alpha }$	$\beta ={90}^{\circ }-\alpha$

3.2.1.2 一般 (斜) 平面三角形中的计算

1. 基本公式

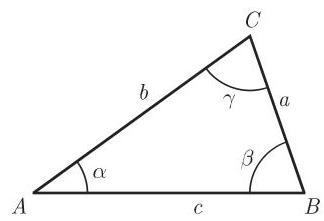
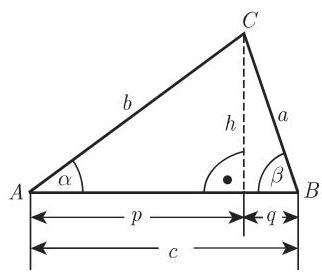
记号 (图 3.33): $a,b,c$ 为边; $\alpha ,\beta ,\gamma$ 为它们所对的角; $S$ 为面积; $R$ 为外接圆半径; $r$ 为内切圆半径; $s=\frac{a+b+c}{2}$ 为半周长.

轮换 由于斜三角形不具有特殊的边或角, 所以从每个包含边和角的公式出发, 有可能按照图 3.34 通过边和角的轮换得到另外两个公式.

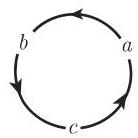
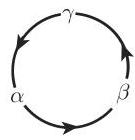
• 从 $\frac{a}{b}=\frac{\sin \alpha }{\sin \beta }$ (正弦定律) 出发,可以通过轮换得到: $\frac{b}{c}=\frac{\sin \beta }{\sin \gamma },\frac{c}{a}=\frac{\sin \gamma }{\sin \alpha }$ .

正弦定律

$$\begin{array}{}\text{(3.88)}& \frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R.\end{array}$$

投影法则(图 3.35)

$$\begin{array}{}\text{(3.89)}& c=a\cos \beta +b\cos \alpha .\end{array}$$

余弦定律或一般三角形的毕达哥拉斯定理

$$\begin{array}{}\text{(3.90)}& c^2=a^2+b^2-2ab\cos \gamma .\end{array}$$

莫尔韦德等式

$$\begin{array}{}\text{(3.91a)}& \left(a+b\right)\sin \frac{\gamma }{2}=c\cos \left(\frac{\alpha -\beta }{2}\right),\end{array}$$$$\begin{array}{}\text{(3.91b)}& \left(a-b\right)\cos \frac{\gamma }{2}=c\sin \left(\frac{\alpha -\beta }{2}\right).\end{array}$$

正切定律

$$\begin{array}{}\text{(3.92)}& \frac{a+b}{a-b}=\frac{\tan \frac{\alpha +\beta }{2}}{\tan \frac{\alpha -\beta }{2}}.\end{array}$$

半角公式

$$\begin{array}{}\text{(3.93)}& \tan \frac{\alpha }{2}=\sqrt{\frac{\left(s-b\right)\left(s-c\right)}{s\left(s-a\right)}}.\end{array}$$

正切公式

$$\begin{array}{}\text{(3.94)}& \tan \alpha =\frac{a\sin \beta }{c-a\cos \beta }=\frac{a\sin \gamma }{b-a\cos \gamma }.\end{array}$$

附加关系

$$\begin{array}{}\text{(3.95a)}& \sin \frac{\alpha }{2}=\sqrt{\frac{\left(s-b\right)\left(s-c\right)}{bc}},\end{array}$$$$\begin{array}{}\text{(3.95b)}& \cos \frac{\alpha }{2}=\sqrt{\frac{s\left(s-a\right)}{bc}}.\end{array}$$

边 $a$ 对应的高

$$\begin{array}{}\text{(3.96)}& h_a=b\sin \gamma =c\sin \beta .\end{array}$$

边 $a$ 的中线

$$\begin{array}{}\text{(3.97)}& m_a=\frac{1}{2}\sqrt{b^2+c^2+2bc\cos \alpha }.\end{array}$$

角 $\alpha$ 的平分线

$$\begin{array}{}\text{(3.98)}& l_{\alpha }=\frac{2bc\cos \frac{\alpha }{2}}{b+c}.\end{array}$$

外接圆半径

$$\begin{array}{}\text{(3.99)}& R=\frac{a}{2\sin \alpha }=\frac{b}{2\sin \beta }=\frac{c}{2\sin \gamma }.\end{array}$$

内切圆半径

$$\begin{array}{}\text{(3.100)}& r=\sqrt{\frac{\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s}}=s\tan \frac{\alpha }{2}\tan \frac{\beta }{2}\tan \frac{\gamma }{2}\end{array}$$$$\begin{array}{}\text{(3.101)}& =4R\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}\text{.}\end{array}$$

面积

$$\begin{array}{}\text{(3.102)}& S=\frac{1}{2}ab\sin \gamma =2R^2\sin \alpha \sin \beta \sin \gamma =rs=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}.\end{array}$$

公式 $S=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$ 称为海伦公式.

2. 一般三角形中边、角和面积的计算

根据全等定理 (参见第 175 页 3.1.3.2), 一个三角形由三个独立的量确定. 其中必须至少有一边.

由此推出四个所谓的基本问题. 如果从六个定义量 (三个角 $\alpha ,\beta ,\gamma$ 和它们所对的边 $a,b,c)$ 出发给定三个独立的量,那么我们就能用表 3.4 中的等式计算剩下的三个量.

	已知量	用于计算其他量的公式
(1)	1 边及 2 角 $\left(a,\alpha ,\beta \right)$	$\gamma ={180}^{\circ }-\alpha -\beta ,b=\frac{a\sin \beta }{\sin \alpha },$ $c=\frac{a\sin \gamma }{\sin \alpha },S=\frac{1}{2}ab\sin \gamma .$
(2)	2 边及其夹角 $\left(a,b,\gamma \right)$	$\tan \frac{\alpha -\beta }{2}=\frac{a-b}{a+b}\cot \frac{\gamma }{2},\frac{\alpha +\beta }{2}={90}^{\circ }-\frac{1}{2}\gamma ;$ $\alpha$ 和 $\beta$ 来自 $\alpha +\beta$ 和 $\alpha -\beta$ , $c=\frac{a\sin \gamma }{\sin \alpha },S=\frac{1}{2}ab\sin \gamma .$
(3)	2边及其中一 边的对角 $\left(a,b,\alpha \right)$	$\sin \beta =\frac{b\sin \alpha }{a},$ 如果 $a\ge b$ 成立,则有 $\beta <{90}^{\circ }$ 并且是唯一确定的. 如果 $a<b$ 成立,则出现下列情形: ① 对于 $b\sin \alpha <a$ 来说, $\beta$ 有两个值 $\left({\beta }_2={180}^{\circ }-{\beta }_1\right)$ ② 对于 $b\sin \alpha =a$ 来说, $\beta$ 恰有一个值 $\left({90}^{\circ }\right)$ . ③ 对于 $b\sin \alpha >a$ 来说,不存在这样的三角形. $\gamma ={180}^{\circ }-\left(\alpha +\beta \right),c=\frac{a\sin \gamma }{\sin \alpha },S=\frac{1}{2}ab\sin \gamma .$
(4)	3 边(a, b, c)	$r=\sqrt{\frac{\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s}},$ $\tan \frac{\alpha }{2}=\frac{r}{s-a},\tan \frac{\beta }{2}=\frac{r}{s-b},\tan \frac{\gamma }{2}=\frac{r}{s-c},$ $S=rs=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}.$

与球面三角学 (参见第 229 页表 3.9 中第二基本问题) 形成对照, 在一个平面三角形中任何一边都无法只从角得到.