13.3.2 面积分

13.3.2.1 平面片向量

一般型的面积分 (参见第 692 页 8.3.4.2) 的向量表示要求对一个平面区域 $S$ 指定一个向量 $\overrightarrow{S}$ ,它垂直于这个区域,并且其绝对值等于 $S$ 的面积. 图 13.16(a) 展示了一个平面片的情形. 根据右手定律 (right-hand law) (也称为右旋法则 (right-screw rule)) 定义沿一条闭曲线 $C$ 的正指向来给出 $S$ 的正方向: 从向量 $\overrightarrow{S}$ 的起始点向其终点看去, 则正指向 (positive sense) 就是顺时针方向. 由边界曲线定向的这个选择就确定了这个曲面区域的外边,即向量 $\overrightarrow{S}$ 所在的那一边. 这个定义对于由一条闭曲线所界的任意曲面区域的情形都有效 (图 13.16(b),(c)).

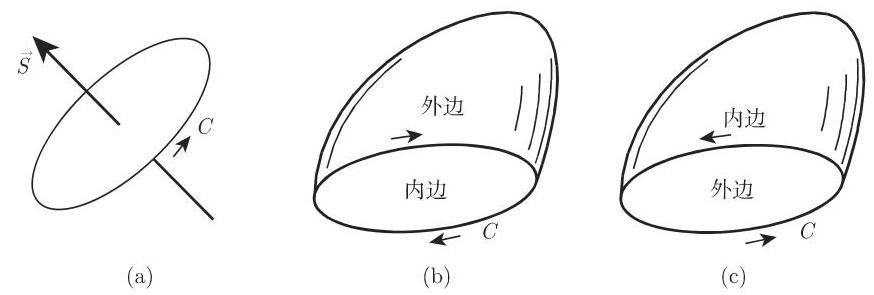
13.3.2.2 面积分的计算

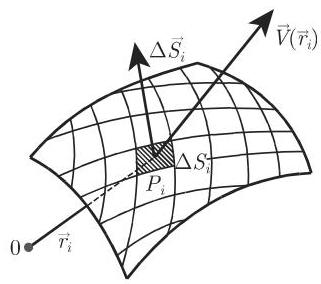
标量场或向量场中一个面积分的计算与曲面 $S$ 是否由一条闭曲线所界或它本身就是一个闭曲面无关. 计算分 5 个步骤:

a) 在 $S$ 的边界曲线定向所定义的外边把曲面区域 $S$ 分成 $n$ 个任意的基本曲面 $\mathrm{\Delta }{S}_i$ (图 13.17),使得这些面元都可被平面元素所逼近. 如在 (13.33a) 中给出的那样,对每个面元 $\mathrm{\Delta }{S}_i$ 指定一个向量 $\mathrm{\Delta }{\overrightarrow{S}}_i$ . 在闭曲面的情形,定义 $\mathrm{\Delta }{\overrightarrow{S}}_i$ 的正方向, 使得 $S$ 的外边是其出发之处.

b) 在每个面元的内点集或边界上任取一点 $P_i$ ,其位置向量为 ${\overrightarrow{r}}_i$ .

c) 在标量场的情形作乘积 $U\left({\overrightarrow{r}}_i\right)\mathrm{\Delta }{\overrightarrow{S}}_i$ ,在向量场的情形作乘积 $\overrightarrow{V}\left({\overrightarrow{r}}_i\right)\cdot \mathrm{\Delta }{\overrightarrow{S}}_i$ 或$\overrightarrow{V}\left({\overrightarrow{r}}_i\right)\times \mathrm{\Delta }{\overrightarrow{S}}_i.$

d) 取所有这些积之和.

e) 当 $\mathrm{\Delta }{S}_i$ 的直径趋于零,即当 $\left|\mathrm{\Delta }{\overrightarrow{S}}_i\right|\to 0$ 时,亦当 $n\to \mathrm{\infty }$ 时计算和之极限. 因而, 对于二重积分, 在第 694 页 8.4.1.1, 1. 中给出的意义下面元趋于零.

如果这个极限的存在与曲面 $S$ 的划分以及点 ${\overrightarrow{r}}_i$ 的选取无关,则称此极限为在给定曲面上 $\overrightarrow{V}$ 的面积分.

13.3.2.3 面积分和场流

1. 标量场的向量流

$$\begin{array}{}\text{(13.113)}& \overrightarrow{P}=\underset{\begin{array}{c}\left|\mathrm{\Delta }{\overrightarrow{S}}_i\right|\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^{n}U\left({\overrightarrow{r}}_i\right)\mathrm{\Delta }{\overrightarrow{S}}_i={\int }_{S}U\left(\overrightarrow{r}\right)\mathrm{d}\overrightarrow{S}.\end{array}$$

2. 向量场的标量流

$$\begin{array}{}\text{(13.114)}& Q=\underset{\begin{array}{c}\left|\mathrm{\Delta }{\overrightarrow{S}}_i\right|\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^n\overrightarrow{V}\left({\overrightarrow{r}}_i\right)\cdot \mathrm{\Delta }{\overrightarrow{S}}_i={\int }_S\overrightarrow{V}\left(\overrightarrow{r}\right)\cdot \mathrm{d}\overrightarrow{S}.\end{array}$$

3. 向量场的向量流

$$\begin{array}{}\text{(13.115)}& \overrightarrow{R}=\underset{\begin{array}{c}\left|\mathrm{\Delta }{\overrightarrow{S}}_i\right|\to 0\\ n\to \mathrm{\infty }\end{array}}{lim}\sum _{i=1}^n\overrightarrow{V}\left({\overrightarrow{r}}_i\right)\times \mathrm{\Delta }{\overrightarrow{S}}_i={\int }_S\overrightarrow{V}\left(\overrightarrow{r}\right)\times \mathrm{d}\overrightarrow{S}.\end{array}$$

13.3.2.4 笛卡儿坐标系中作为第二型面积分的面积分

$$\begin{array}{}\text{(13.116)}& {\int }_{S}U\mathrm{d}\overrightarrow{S}={\iint }_{S_{yz}}U\mathrm{d}y\mathrm{d}z\overrightarrow{i}+{\iint }_{S_{zx}}U\mathrm{d}z\mathrm{d}x\overrightarrow{j}+{\iint }_{S_{xy}}U\mathrm{d}x\mathrm{d}y\overrightarrow{k}.\end{array}$$$$\begin{array}{}\text{(13.117)}& {\int }_S\overrightarrow{V}\cdot \mathrm{d}\overrightarrow{S}={\iint }_{S_{yz}}{V}_x\mathrm{d}y\mathrm{d}z+{\iint }_{S_{zx}}{V}_y\mathrm{d}z\mathrm{d}x+{\iint }_{S_{xy}}{V}_z\mathrm{d}x\mathrm{d}y.\end{array}$$$${\int }_S\overrightarrow{V}\times \mathrm{d}\overrightarrow{S}={\iint }_{S_{yz}}\left(V_z\overrightarrow{j}-V_y\overrightarrow{k}\right)\mathrm{d}y\mathrm{d}z+{\iint }_{S_{zx}}\left(V_x\overrightarrow{k}-V_z\overrightarrow{i}\right)\mathrm{d}z\mathrm{d}x$$$$\begin{array}{}\text{(13.118)}& +{\iint }_{S_{xy}}\left(V_y\overrightarrow{i}-V_x\overrightarrow{j}\right)\mathrm{d}x\mathrm{d}y.\end{array}$$

类似于第 710 页 8.5.2.1,4. 中的存在性定理, 可以给出关于这些积分的存在性定理. 在上面这些公式中,每个积分被展布在 $S$ 在相应的坐标平面的投影上 (图 13.18),在每个投影上变量 $x,y,z$ 之一要根据 $S$ 的方程由其他两个变量来表示.

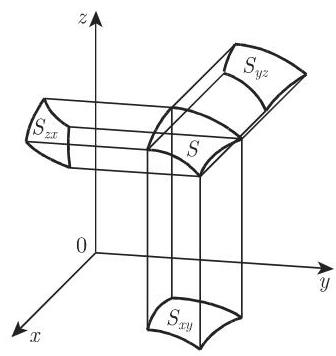
注 用下列式子表示在闭曲面上的积分:

$$\begin{array}{}\text{(13.119)}& {\oint }_{S}U\mathrm{d}\overrightarrow{S}={\text{oiint}}_{S}U\mathrm{d}\overrightarrow{S},{\oint }_S\overrightarrow{V}\cdot \mathrm{d}\overrightarrow{S}={\text{oiint}}_S\overrightarrow{V}\cdot \mathrm{d}\overrightarrow{S},{\oint }_S\overrightarrow{V}\times \mathrm{d}\overrightarrow{S}={\text{oiint}}_S\overrightarrow{V}\times \mathrm{d}\overrightarrow{S}.\end{array}$$

$◼\mathbf{A}$: 计算积分 $\overrightarrow{P}={\int }_{S}xyz\mathrm{d}\overrightarrow{S}$ ,其中曲面 $S$ 是由 3 个坐标平面所围的平面区域 $x+y+z=1$ . 其向上的边是正边:

$$\overrightarrow{P}={\iint }_{S_{yz}}\left(1-y-z\right)yz\mathrm{d}y\mathrm{d}z\overrightarrow{i}+{\iint }_{S_{zx}}\left(1-x-z\right)xz\mathrm{d}z\mathrm{d}x\overrightarrow{j}+{\iint }_{S_{xy}}\left(1-x-y\right)xy\mathrm{d}x\mathrm{d}y\overrightarrow{k};$$$${\iint }_{S_{yz}}\left(1-y-z\right)yz\mathrm{d}y\mathrm{d}z={\int }_0^1{\int }_0^{1-z}\left(1-y-z\right)yz\mathrm{d}y\mathrm{d}z=\frac{1}{120}.$$

可以类似地求另两个积分. 结果为: $\overrightarrow{P}=\frac{1}{120}\left(\overrightarrow{i}+\overrightarrow{j}+\overrightarrow{k}\right)$ .

$◼\mathbf{B}$: 在如A中同一平面区域上计算积分 $Q={\int }_S\overrightarrow{r}\cdot \mathrm{d}\overrightarrow{S}={\iint }_{S_{yz}}x\mathrm{d}y\mathrm{d}z+$ ${\iint }_{S_{zx}}y\mathrm{d}z\mathrm{d}x+{\iint }_{S_{xy}}z\mathrm{d}x\mathrm{d}y.{\iint }_{S_{yz}}x\mathrm{d}y\mathrm{d}z={\int }_0^1{\int }_0^{1-z}\left(1-y-z\right)\mathrm{d}y\mathrm{d}z=\frac{1}{6}$ . 可以类似地求另两个积分. 结果为: $Q=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}$ .

$◼\mathbf{C}$: 在如A中同一平面区域上计算积分 $\overrightarrow{R}={\int }_S\overrightarrow{r}\times \mathrm{d}\overrightarrow{S}={\int }_S\left(x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}\right)\times$ $\left(\mathrm{d}y\mathrm{d}z\overrightarrow{i}+\mathrm{d}z\mathrm{d}x\overrightarrow{j}+\mathrm{d}x\mathrm{d}y\overrightarrow{k}\right)$ . 计算后给出 $\overrightarrow{R}=\overrightarrow{0}$ .