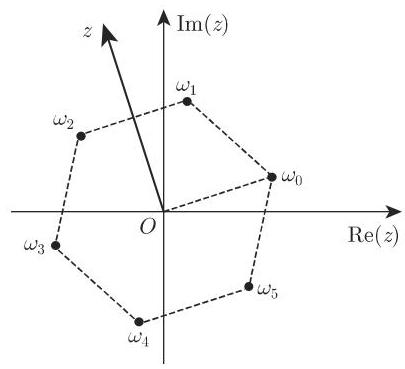
Appearance
1.5.3 复数的计算
1.5.3.1 加法和减法
以代数形式给出的两个或多个复数的加法和减法, 定义如下:
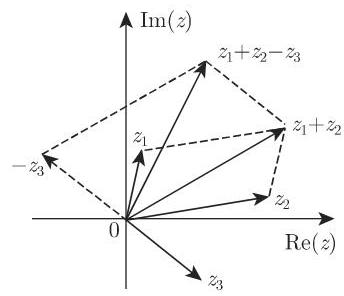
上述计算与一般二项式的处理方式相同. 对加法和减法进行几何解释可考虑对应向量的加减法 (图 1.8), 一般的向量计算法则对复数都适用 (参见第 242 页 3.5.1.1). 对于
1.5.3.2 乘法
以代数形式给出的两个复数
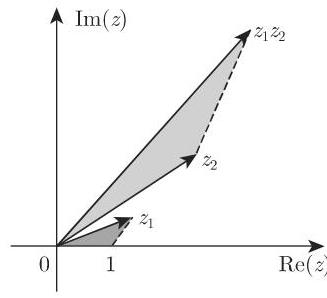
若复数以三角形式给出, 则有
即乘积的模等于各因子的模之积, 积的辐角等于各因子的辐角之和.
积的指数形式为
两个复数
积
对于
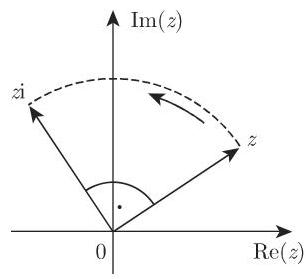
1.5.3.3 除法
除法定义为乘法的逆运算. 对于以代数形式给出的复数, 有
若复数以三角形式给出, 则有
即商的模等于被除数和除数模的比值; 商的辐角等于两辐角之差.
对于指数形式, 有
向量
注 除以零向量不存在.
1.5.3.4 基本运算法则
关于复数
是一个实数.
1.5.3.5 复数的幂
复数的
即幂的模是
一般地,
1.5.3.6 复数的
求复数的
是
的简单记法. 复数的加、减、乘、除和整数次幂,都有唯一结果,而
点