Appearance
18.2.7 不等式类型约束下问题的梯度法
如果问题
需要采用如下类型的迭代法求解:
那么由于有界可行集, 必须考虑另两个附加规则:
(1) 方向
(2) 步长
基于公式 (18.96) 的各种方法的差别仅在于构造方向
然后, 我们得到
如果在某一步
18.2.7.1 可行方向方法
1. 方向搜索程序
点
如果
由(18.100a,18.100b,18.100c)定义的方向搜索程序有可能引起序列
即代之以在
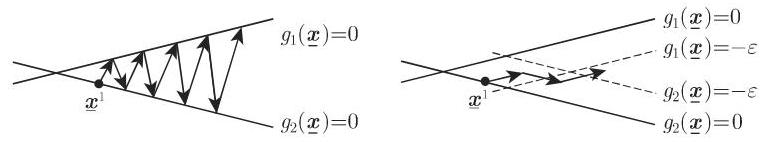
如果
2. 线性约束的特殊情形
如果
其中
选择不同范数
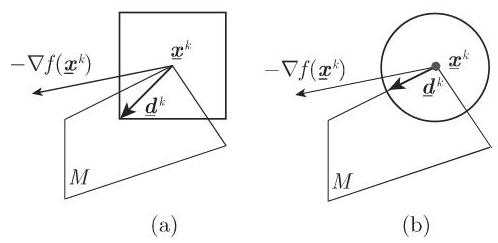
在某种意义上,范数
为了确保这种可行方向方法对于二次优化问题
条件
此外,前面各步骤中相应的的条件均保留不变. 如果在往后的某一步有
第 1 步: 从
方向搜索程序:
最小化常数:
最大可行步长:
第 2 步:
方向搜索程序:
第 3 步:
方向搜索程序:
接下来的方向搜索程序结果是
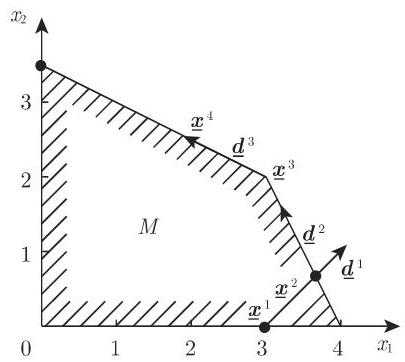
18.2.7.2 梯度投影方法
1. 问题的提法和求解原理
假定给定凸优化问题
点
如果
就给出这样的投影. 这里
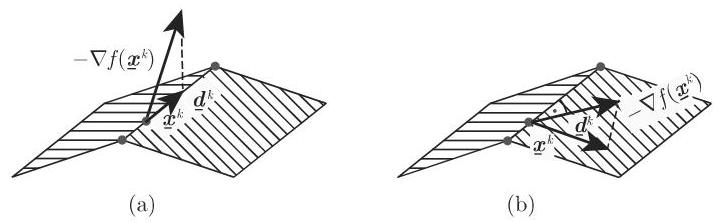
2. 算法
梯度投影法由如下几个步骤组成: 从
如果
3. 关于算法的注释
如果
第 1 步:
第 2 步:
第 3 步:
第 4 步:
由此可知,