Appearance
18.1.1 问题的提法和几何表达
18.1.1.1 线性规划问题的形式
1. 目的
线性规划的目的是寻找有穷个变量的线性目标函数(OF) 在有穷个线性方程或不等式约束(CT) 限制下的最大值或最小值.
许多实际问题都可以直接叙述为线性规划问题, 或者用线性规划问题近似建模.
2. 一般形式线性规划问题的一般形式是
OF:
(18.1b)
采用更紧凑的向量记号, 上述问题可以写成
OF:
这里使用如下记号:
3. 约束
对于不等号 “
4. 极小问题
对于极小问题
5. 整数规划
有时候某些变量仅限于取整数值. 这里我们不讨论这样的离散问题.
6. 仅含非负变量和松弛变量情形的表达
在应用某些解法时, 仅仅考虑非负变量, 以及以等式形式给出的约束 (18.1b) 和 (18.2b).
每个自由变量
OF:
CT:
一般可以假定
7. 可行集
所有满足 (18.2b) 的向量集合称作原问题的可行集. 如果自由变量做如上改写, 每个形如 “
如果点
则
18.1.1.2 例子和图解法
1. 生产两个产品的例子
假定为了生产两个产品
表 18.1
12 | 8 | 0 | |
6 | 12 | 10 | |
总数 | 630 | 620 | 350 |
售出一个单位
现在设
OF:
引入松弛变量
CT:
2. 线性规划问题的性质
基于这个例子, 可以用图表示法来说明线性规划问题的某些性质. 这里不考虑松弛变量, 仅使用原始变量.
a) 直线
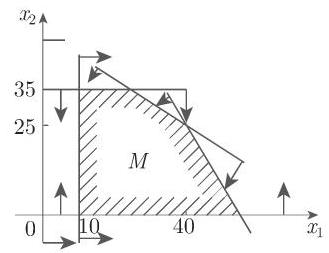
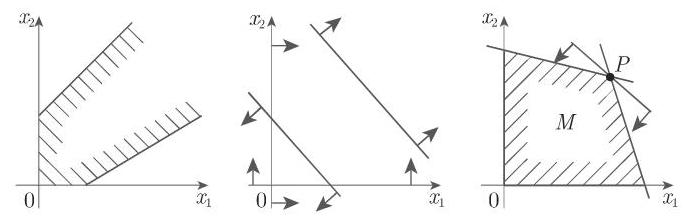
b)
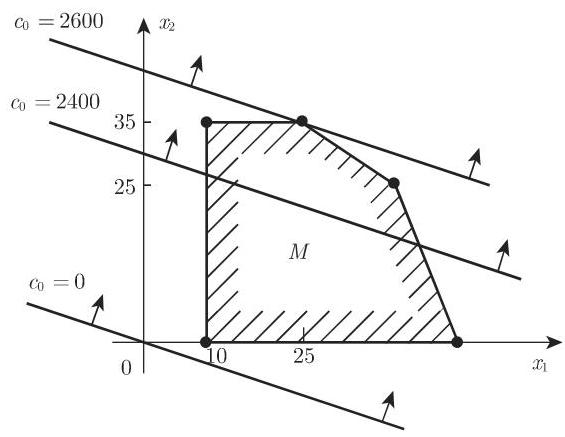
显然,如果可行集