14.6.2 雅可比函数

1. 定义

对于第一类椭圆积分 $F\left(k,\phi \right)$ ,当 $0<k<1$ 时从表达式 (8.24a) 和 (8.25a) (参见第 653 页 8.1.4.3) 即得

$$\begin{array}{}\text{(14.103)}& \frac{\mathrm{d}F}{\mathrm{d}\phi }={(1-k^2{\sin }^2\phi )}^{-\frac{1}{2}}>0,\end{array}$$

即, $F\left(k,\phi \right)$ 关于 $\phi$ 是严格单调的,因而 (14.104b) 的反函数 (14.104a) 存在:

$$\begin{array}{}\text{(14.104a)}& \phi =\mathrm{am}\left(k,u\right)=\phi \left(u\right),\end{array}$$$$\begin{array}{}\text{(14.104b)}& u={\int }_0^{\phi }\frac{\mathrm{d}\psi }{\sqrt{1-k^2{\sin }^2\psi }}=u\left(\phi \right).\end{array}$$

此反函数被称为振幅函数 (amplitude function). 所谓的雅可比函数 (Jacobian functions) 被定义为

$$\begin{array}{}\text{(14.105a)}& \mathrm{sn}u=\sin \phi =\sin \mathrm{am}\left(k,u\right)\text{ (振幅正弦),}\end{array}$$$$\begin{array}{}\text{(14.105b)}& \mathrm{cn}u=\cos \phi =\cos \mathrm{am}\left(k,u\right)\text{(振幅余弦),}\end{array}$$$$\begin{array}{}\text{(14.105c)}& \mathrm{dn}u=\sqrt{1-k^2{\mathrm{sn}}^{2}u}\text{ (振幅 }\delta \text{ ). }\end{array}$$

2. 亚纯函数和双周期函数

雅可比函数可以被解析延拓到 $z$ 平面. 因而诸函数 $\mathrm{sn}z,\mathrm{cn}z,\mathrm{dn}z$ 都是亚纯 (meromorphic) 函数 (参见第 983 页 14.3.5.2), 即, 它们的奇点只是极点. 除此之外,它们是双周期的 (double periodic). 这些函数 $f\left(z\right)$ 中的每一个都恰有两个周期 ${\omega }_1$ 和 ${\omega }_2$ ,满足

$$\begin{array}{}\text{(14.106)}& f\left(z+{\omega }_1\right)=f\left(z\right),f\left(z+{\omega }_2\right)=f\left(z\right).\end{array}$$

这里, ${\omega }_1$ 和 ${\omega }_2$ 是两个其比值不是实数的任意复数. 从 (14.106) 即得一般公式

$$\begin{array}{}\text{(14.107)}& f\left(z+m{\omega }_1+n{\omega }_2\right)=f\left(z\right),\end{array}$$

其中 $m$ 和 $n$ 是任意整数. 全纯的双周期函数被称为椭圆函数 (elliptic functions). 设 $z_0\in \mathbb{C}$ 为一个任意的固定点,则集合

$$\begin{array}{}\text{(14.108)}& \left\{z_0+{\alpha }_1{\omega }_1+{\alpha }_2{\omega }_2:0\le {\alpha }_1,{\alpha }_2<1\right\}\end{array}$$

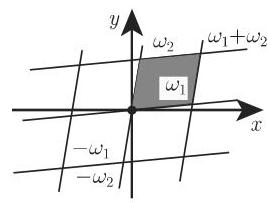
被称为椭圆函数的周期平行四边形 (period parallelogram). 如果双周期函数在整个周期平行四边形 (图 14.55) 中是有界的, 那么它是一个常数.

$◼$ 雅可比函数 (14.105a) 和 (14.105b) 是椭圆函数. 振幅函数 (14.104a) 不是椭圆函数.

3. 雅可比函数的性质

由下述代换

$$\begin{array}{}\text{(14.109)}& k^{\prime 2}=1-k^2,K^{\prime }=F\left(k^{\prime },\frac{\pi }{2}\right),K=F\left(k,\frac{\pi }{2}\right)\end{array}$$

可以得到在表 14.3 中给出的雅可比函数的那些性质,其中 $m$ 和 $n$ 是任意整数.

	周期 ${\omega }_1,{\omega }_2$	根	极点
$\mathrm{sn}z$	$4K,2\mathrm{i}{K}^{\prime }$	$2mK+2n\mathrm{i}{K}^{\prime }$
$\mathrm{cn}z$	$4K,2\left(K+\mathrm{i}{K}^{\prime }\right)$	$\left(2m+1\right)K+2n\mathrm{i}{K}^{\prime }$	$2mK+\left(2n+1\right)\mathrm{i}{K}^{\prime }$
$\mathrm{dn}z$	$2K,4\mathrm{i}{K}^{\prime }$	$\left(2m+1\right)K+\left(2n+1\right)\mathrm{i}{K}^{\prime }$

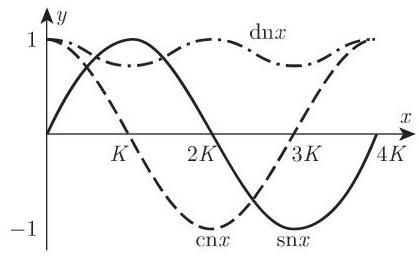
图 14.56 中有函数 $\mathrm{sn}z,\mathrm{cn}z$ 和 $\mathrm{dn}z$ 的图形. 除了在极点处外,下列关系式对雅可比函数成立:

(1) ${\mathrm{sn}}^{2}z+{\mathrm{cn}}^{2}z=1,k^2{\mathrm{sn}}^{2}z+{\mathrm{dn}}^{2}z=1$ ,(14.110)

(2) $\mathrm{sn}\left(u+v\right)=\frac{\left(\mathrm{sn}u\right)\left(\mathrm{cn}v\right)\left(\mathrm{dn}v\right)+\left(\mathrm{sn}v\right)\left(\mathrm{cn}u\right)\left(\mathrm{dn}u\right)}{1-k^2\left({\mathrm{sn}}^{2}u\right)\left({\mathrm{sn}}^{2}v\right)}$ ,(14.111a)

$$\begin{array}{}\text{(14.111b)}& \mathrm{cn}\left(u+v\right)=\frac{\left(\mathrm{cn}u\right)\left(\mathrm{cn}v\right)-\left(\mathrm{sn}u\right)\left(\mathrm{dn}u\right)\left(\mathrm{sn}v\right)\left(\mathrm{dn}v\right)}{1-k^2\left({\mathrm{sn}}^{2}u\right)\left({\mathrm{sn}}^{2}v\right)},\end{array}$$$$\begin{array}{}\text{(14.111c)}& \mathrm{dn}\left(u+v\right)=\frac{\left(\mathrm{dn}u\right)\left(\mathrm{dn}v\right)-k^2\left(\mathrm{sn}u\right)\left(\mathrm{cn}u\right)\left(\mathrm{sn}v\right)\left(\mathrm{cn}v\right)}{1-k^2\left({\mathrm{sn}}^{2}u\right)\left({\mathrm{sn}}^{2}v\right)},\end{array}$$

(3) ${\left(\mathrm{sn}z\right)}^{\prime }=\left(\mathrm{cn}z\right)\left(\mathrm{dn}z\right)$ ,(14.112a)

$$\begin{array}{}\text{(14.112b)}& {\left(\mathrm{cn}z\right)}^{\prime }=-\left(\mathrm{sn}z\right)\left(\mathrm{dn}z\right),\end{array}$$$$\begin{array}{}\text{(14.112c)}& {\left(\mathrm{dn}z\right)}^{\prime }=-k^2\left(\mathrm{sn}z\right)\left(\mathrm{cn}z\right).\end{array}$$

雅可比函数的其他性质和另一些椭圆函数见 [14.10], [14.18].