5.8.5 可平面图

因为有向图是可平面图, 当且仅当相应的无向图是可平面图, 所以我们在此限于考虑无向图.

1. 可平面图

图 $G$ 称为平面图,当且仅当 $G$ 可以画在一个平面上,并且它的边仅在 $G$ 的顶点相交. 与平面图同构的图称作可平面图.

图 5.56 给出平面图 $G_1$ . 图 5.57 中的图 $G_2$ 同构于 $G_1$ ,它不是平面图,但是一个可平面图,因为它与 $G_1$ 同构.

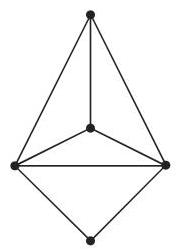
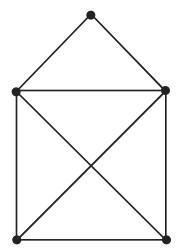
2. 非可平面图

完全图 $K_5$ 和完全二部图 $K_{3,3}$ 是非可平面图.

3. 细分

如果将二次顶点插入 $G$ 的边中,那么我们就可得到图 $G$ 的一个细分. 每个图都是它自身的细分. 图 5.58 和图 5.59 给出 $K_5$ 和 $K_{3,3}$ 的某些细分.

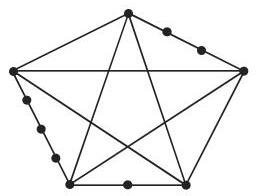
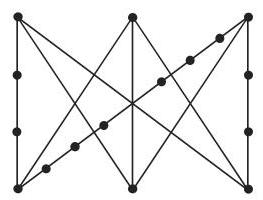
4. 库拉托夫斯基 (Kuratowski) 定理

一个图是非可平面的,当且仅当它含有一个子图是完全二部图 $K_{3,3}$ 或完全图 $K_5$ 的细分.