Appearance
13.1.3 向量场
13.1.3.1 向量场或向量点函数
如果对于空间一个子集的每个点
并称 (13.12a) 为一个向量场 (vector field).
一个向量场
其中
13.1.3.2 一些重要的向量场
1. 中心向量场
在一个中心向量场中,所有向量
把极点置为该中心, 则向量场由公式
所表示,该场的所有向量与径向量
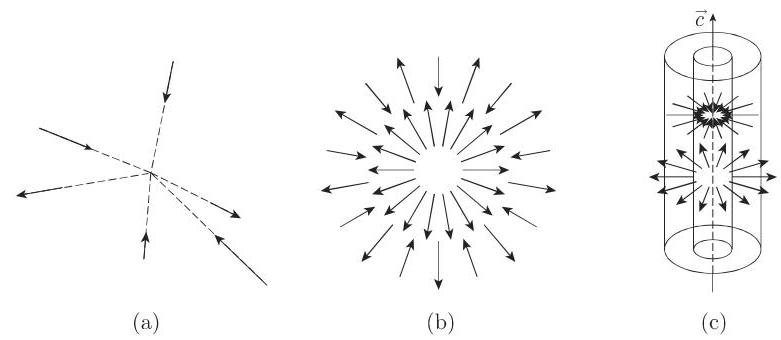
定义向量场常会有某些便利,其中
2. 球面向量场
球面向量场是中心向量场的一个特殊情形,其中向量
平面球面向量场的特殊情形被称为一个圆场(circular field).
3. 柱面向量场
a) 所有向量
b) 离轴有同样距离的点处的所有向量
把极点置于平行于单位向量
其中
用垂直于轴的平面截这个向量场, 总是得到相同的圆场.
13.1.3.3 向量场的坐标表示
1. 笛卡儿坐标系中的向量场
向量场 (13.12a) 可以由标量场
利用坐标单位向量
因而, 可以借助于 3 个标量变量的 3 个标量函数来定义向量场.
2. 柱面坐标系和球面坐标系中的向量场
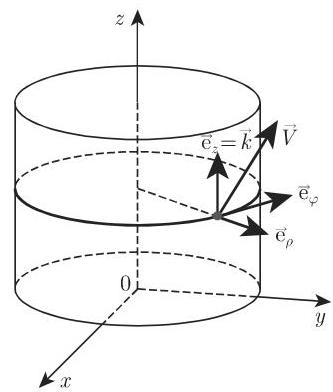
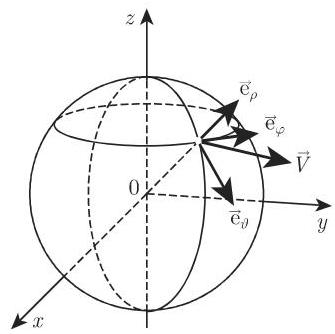
在柱面坐标系和球面坐标系中, 坐标单位向量
在各点处切于坐标线 (图 13.6, 图 13.7). 在这个次序下, 它们总是形成一个右手坐标系. 诸系数被表示为相应坐标的函数:
在从一点转移到另一点时, 诸坐标单位向量改变其方向, 但仍保持相互垂直.
13.1.3.4 坐标系变换
亦见表 13.1.
笛卡儿坐标系 | 柱面坐标系 | 球面坐标系 |
1. 用柱面坐标系表示笛卡儿坐标系
2. 用笛卡儿坐标系表示柱面坐标系
3. 用球面坐标系表示笛卡儿坐标系
4. 用笛卡儿坐标系表示球面坐标系
5. 用笛卡儿坐标系表示球面向量场
6. 用笛卡儿坐标系表示柱面向量场
在球面向量场的情形,球面坐标系,即形式
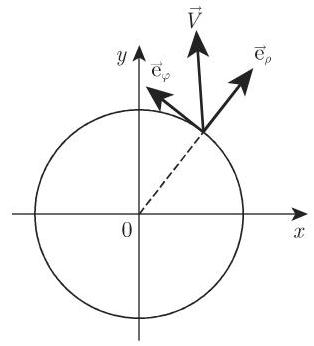
对于圆场, 有
13.1.3.5 向量线
一条曲线
a) 一般的场
b) 平面场
为了解这些微分方程, 请见第 717 页的 9.1.1.2 或第 754 页的 9.2.1.1.
A B: 向量场