6.2.1 偏导数

6.2.1.1 函数的偏导数

$n$ 元函数 $u=f\left(x_1,x_2,\cdots ,x_i,\cdots ,x_n\right)$ 的偏导数,比如关于 $x_1$ 的偏导数定义为

$$\begin{array}{}\text{(6.35)}& \frac{\partial u}{\partial x_1}=\underset{\mathrm{\Delta }{x}_1\to 0}{lim}\frac{f\left(x_1+\mathrm{\Delta }{x}_1,x_2,x_3,\cdots ,x_n\right)-f\left(x_1,x_2,x_3,\cdots ,x_n\right)}{\mathrm{\Delta }{x}_1},\end{array}$$

即认为 $n$ 个变量中只有一个发生了改变,而其他 $n-1$ 个是常数. 偏导数的符号为 $\frac{\partial u}{\partial x},u_x^{\prime },\frac{\partial f}{\partial x},f_x^{\prime }.n$ 元函数有 $n$ 个一阶偏导数 $\frac{\partial u}{\partial x_1},\frac{\partial u}{\partial x_2},\frac{\partial u}{\partial x_3},\cdots ,\frac{\partial u}{\partial x_n}$ ,且可利用与一元函数相同的求导法则来计算偏导数.

$◼u=\frac{x^{2}y}{z},\frac{\partial u}{\partial x}=\frac{2xy}{z},\frac{\partial u}{\partial y}=\frac{x^2}{z},\frac{\partial u}{\partial z}=-\frac{x^{2}y}{z^2}.$

6.2.1.2 二元函数的几何意义

函数 $u=f\left(x,y\right)$ 在笛卡儿坐标系中表示一曲面,过曲面上一点 $P$ 作平行于 $uOx$ 面的平面与之相交 (图 6.14),则

$$\begin{array}{}\text{(6.36a)}& \frac{\partial u}{\partial x}=\tan \alpha \end{array}$$

其中 $\alpha$ 为上述平面与曲面的交曲线在点 $P$ 的切线与 $x$ 轴正半轴所成的角,它也等于切线在 $uOx$ 面的垂直投影与 $x$ 轴正半轴所成的角, $\alpha$ 的正方向为从 $x$ 轴正半轴出发,朝 $y$ 轴正半轴方向看的逆时针方向. 类似 $\alpha$ ,可以用平行于 $yOu$ 的平面定义角 $\beta$ :

$$\begin{array}{}\text{(6.36b)}& \frac{\partial u}{\partial y}=\tan \beta \end{array}$$

关于给定方向的导数, 即所谓的方向导数, 以及关于空间的导数将在向量分析中讨论 (参见第 925 页 13.2.1.3).

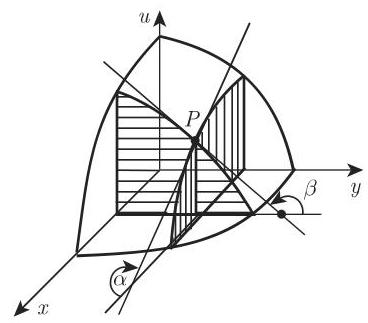
6.2.1.3 $x$ 和 $f\left(x\right)$ 的微分

(1) 自变量 $x$ 的微分 $\mathrm{d}x$ 等于增量 $\mathrm{\Delta }x$ ,即

$$\begin{array}{}\text{(6.37a)}& \mathrm{d}x=\mathrm{\Delta }x,\end{array}$$

其中 $\mathrm{\Delta }x$ 为任意量.

(2) 含一个变量 $x$ 的函数 $y=f\left(x\right)$ 的微分 $\mathrm{d}y$ : 对给定的 $x$ 及 $\mathrm{d}x$ ,定义

$$\begin{array}{}\text{(6.37b)}& \mathrm{d}y=f^{\prime }\left(x\right)\mathrm{d}x.\end{array}$$

(3) 对 $x+\mathrm{\Delta }x$ ,函数 $y=f\left(x\right)$ 的增量是差

$$\begin{array}{}\text{(6.37c)}& \mathrm{\Delta }y=f\left(x+\mathrm{\Delta }x\right)-f\left(x\right).\end{array}$$

(4) 微分的几何意义:

在笛卡儿坐标系中把函数用一条曲线表示,则 $\mathrm{d}y$ 是当 $x$ 改变 $\mathrm{d}x$ 时,切线纵坐标的增量 (图 6.1),而 $\mathrm{\Delta }y$ 是曲线纵坐标的增量.

6.2.1.4 微分的基本性质

1. 不变性

不管 $x$ 是自变量还是另一个变量 $t$ 的函数,都有

$$\begin{array}{}\text{(6.38)}& \mathrm{d}y=f^{\prime }\left(x\right)\mathrm{d}x.\end{array}$$

2. 量的阶

若 $\mathrm{d}x$ 为任意小量,则 $\mathrm{d}y$ 和 $\mathrm{\Delta }y=y\left(x+\mathrm{\Delta }x\right)-y\left(x\right)$ 也为任意小量,但它们等价,即 $\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{d}y}=1$ . 因此它们的差 $\mathrm{d}y-\mathrm{\Delta }y$ 也为任意小量,而且是比 $\mathrm{d}x,\mathrm{d}y,\mathrm{\Delta }x$ 高阶的任意小 (除非 $\mathrm{d}y=0$ ),故有

$$\begin{array}{}\text{(6.39)}& \underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{d}y}=1,\mathrm{\Delta }y\approx \mathrm{d}y=f^{\prime }\left(x\right)\mathrm{d}x,\end{array}$$

于是可以把对小增量的计算简化到计算它的微分, 这个公式常用于近似计算 (参见第 593 页 6.1.4.4 和 1114 页 16.4.2.1, 2.).

6.2.1.5 偏微分

对多元函数 $u=f\left(x,y,\cdots \right)$ ,可计算其中一个变元的偏微分,例如关于 $x$ 的偏微分可定义为

$$\begin{array}{}\text{(6.40)}& {\mathrm{d}}_{x}u={\mathrm{d}}_{x}f=\frac{\partial u}{\partial x}\mathrm{d}x.\end{array}$$