Appearance
2.8.1 反三角函数的定义
现在针对正弦函数的反函数来说明如何定义反三角函数 (图 2.43), 反正弦函数通常记为
曲线
曲线, 其中定义域和值域分别为
类似地,可以得到其他反三角函数,如图 2.44 时2.44
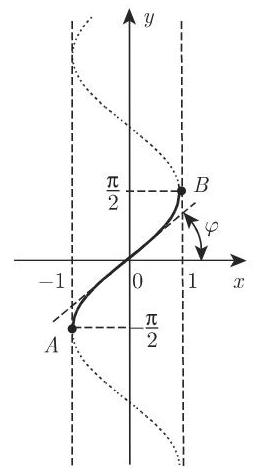
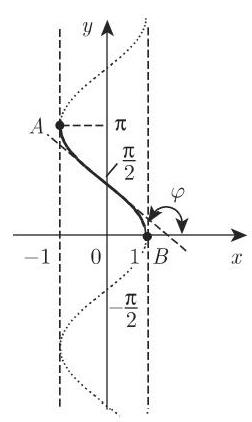
图 2.44 图 2.43
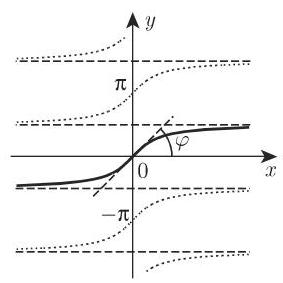
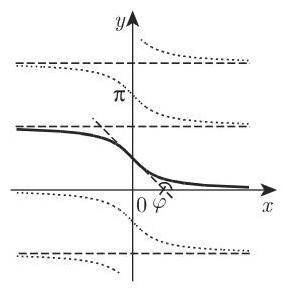
图 2.45 图 2.46
反函数 | 定义域 | 值域 | 具有相同意义的三角函数 |
arcsin | |||
arccos | |||
arctan | |||
arccot |
Appearance
现在针对正弦函数的反函数来说明如何定义反三角函数 (图 2.43), 反正弦函数通常记为
曲线
曲线, 其中定义域和值域分别为
类似地,可以得到其他反三角函数,如图 2.44 时2.44


图 2.44 图 2.43


图 2.45 图 2.46
反函数 | 定义域 | 值域 | 具有相同意义的三角函数 |
arcsin | |||
arccos | |||
arctan | |||
arccot |