Appearance
8.4.1 二重积分
8.4.1.1 二重积分的概念
1. 定义
二元函数
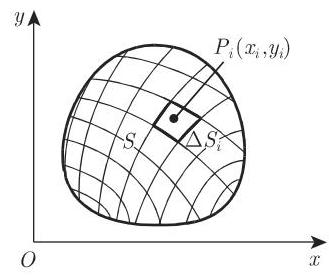
若二重积分存在, 则它是一个数, 且可按下面方法来定义 (图 8.30):
(1) 将区域
(2)在每个小区域的内部或边界任取一点
(3) 用函数在点
(4) 所有乘积
(5) 当每个小区域的直径趋于 0,即
的极限. (点集的直径是指集合中任意两点间距离的上确界. ) 此处仅要求
2. 存在定理
若函数
3. 几何意义
二重积分的几何意义是以
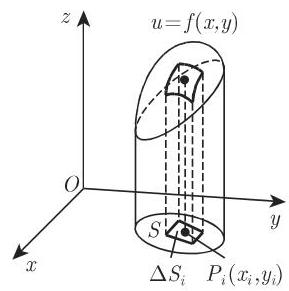
若函数值恒为
8.4.1.2 二重积分的计算
可以把二重积分的计算化成累次积分的计算, 即相继计算两个积分.
1. 笛卡儿坐标系下的计算
若二重积分存在, 可以把积分区域划分成任何类型, 如小矩形. 在用坐标线把积分区域化成无限小的矩形后 (图 8.32(a)), 可先沿小矩形的每个垂直边再沿水平边计算所有微分
其中
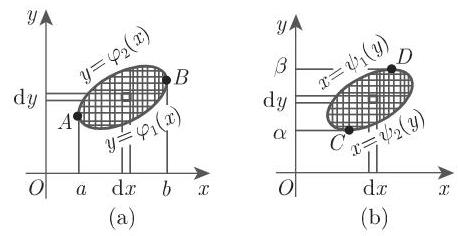
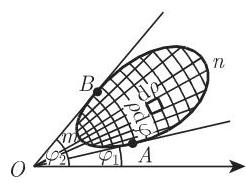
(小矩形的面积等于
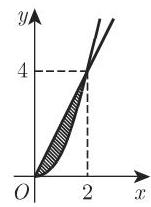
- 计算
,其中 是由抛物线 和直线 围成的平面区域 (图 8.33).
或
2. 极坐标系下的计算
用坐标线把积分区域分成若干个小区域, 每个小区域均以从极点出发的两个同心圆和两条射线为边界 (图 8.34). 极坐标系下小区域的面积具有形式
(对于
其中
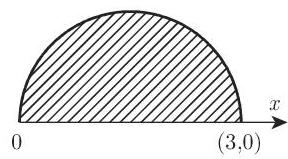
- 计算特殊积分
为半圆面 (图 8.35):
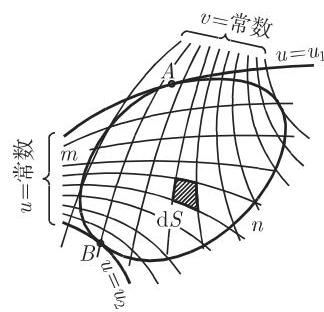
3. 任意曲线坐标系
坐标定义如下:
(参见第 350 页 3.6.3.1). 若坐标线
其中
在曲线坐标系下, 易得小区域的面积
对极坐标
所选择的曲线坐标系应该使 (8.139) 中的积分限尽可能简单, 而且被积函数不要太过复杂.
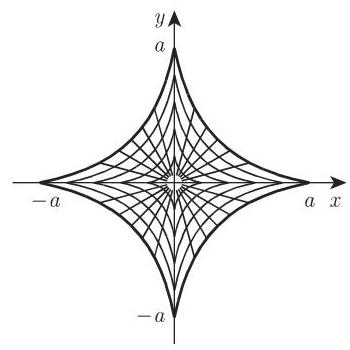
- 计算
为星形线的内部 (参见第 134 页 2.13.4),其中 (图 8.37). 令 ,引入曲线坐标 , 坐标线 表示一族与方程 类似的星形线. 坐标线 是方程为 的射线,其中 . 由此
8.4.1.3 二重积分的应用
表 8.8 给出了笛卡儿坐标系和极坐标系下小区域的面积. 表 8.9 给出了二重积分的某些应用.
坐标 | 面积微元 |
笛卡儿坐标 | |
极坐标 | |
任意曲线坐标 |