9.2.5 非线性偏微分方程: 孤子、周期模式和混沌

9.2.5.1 物理一数学问题的阐述

1. 孤子的概念

孤子 (solitons), 也称为孤波, 从物理学观点看, 是脉冲, 或者也是一种非线性介质或场的局部化扰动; 与这样传播的脉冲或扰动有关的能量集中在一个窄小的空间区域里. 它们出现:

• 在立体中, 例如, 在非谐振晶格中, 在约瑟夫森 (Josephson) 接触中, 在玻璃纤维中和在拟一维导体中,

• 在流体中作为表面波或自旋波,

• 在等离体中作为朗缪尔 (Langmuir) 孤子,

• 在线性分子中,

• 在经典场论和量子场论中.

孤子兼有粒子性质和波性质; 在孤子的演化中它们被局部化了, 并且局部化的区域, 或者围绕着局部化波的点, 如同一个自由粒子那样地行进; 特别地, 它也可以停止. 孤子具有持久波的结构: 基于非线性性和离差之间的平衡, 这个结构的形式不改变.

在数学上, 孤子是出现在物理学、工程学和应用数学中的某些非线性偏微分方程的特解. 它们不寻常的特点是任何耗散的缺失, 以及不能由扰动理论来控制非线性项. 耗散孤子出现在非保守系统中.

2. 具有孤子解的方程的重要例子

a) 科尔泰沃赫-德弗里斯 (Korteweg de Vries, KdV) 方程

$$\begin{array}{}\text{(9.148)}& u_t+6u{u}_x+u_{xxx}=0,\end{array}$$

b) 非线性薛定谔 (NLS) 方程 $\mathrm{i}{u}_t+u_{xx}\pm 2{\left|u\right|}^{2}u=0$ ,(9.149)

c) 正弦戈登 (Gordon, SG) 方程 $u_{tt}-u_{xx}+\sin u=0$ .(9.150)

下标 $x$ 和 $t$ 表示偏导数,例如, $u_{xx}={\partial }^{2}u/\partial x^2$ .

在这些方程中考虑了一维情形,即, $u$ 有形式 $u=u\left(x,t\right)$ ,其中 $x$ 是空间坐标, $t$ 是时间. 这些方程以标量形式给出,即,这里的两个自变量 $x$ 和 $t$ 是无量纲量. 在实际应用中, 它们必须乘以有相应量纲并是所给问题特征的量. 对于速度亦然.

3. 孤子间的相互作用

如果两个以不同速度行进的孤子碰撞了, 在相互作用后它们又出现了, 好像它们未曾碰撞过一样. 每个孤子渐近地保持其形状和速度; 只有一个相移. 两个孤子可以相互作用而渐近地相互间并不干扰. 这被称为弹性相互作用,它等价于一个 $N$ -孤子解的存在性,这里 $N\left(N=1,2,3,\cdots \right)$ 是孤子的数目. 求解给定了分解为数个孤子的初始脉冲 $u\left(x,0\right)$ 的初值问题,孤子的数目并不依赖于脉冲的形状,而依赖于其总量 ${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}u\left(x,0\right)\mathrm{d}x$ .

4. 周期模式和非线性波

这样的非线性现象出现在一些经典的耗散系统 (即摩擦系统或阻尼系统) 中, 如果外部碰撞或外力足够大. 例如, 如果在引力场中有一层流体, 从下面对其加热, 那么在上下表面层之间的温差就相当于一个外力. 下层的较高温度减少了它的密度, 使其轻于其上部, 因而分层就变得不稳定. 到了一个充分大的温差时, 该不稳定层就自发地转为周期的对流晶胞. 它被称为从热导率态 (无对流) 到良序瑞利-贝纳尔 (Bénard) 对流的分岔 (bifurcation) ${}^{\text{①}}$ . 由于耗散进入了波的阻尼 (这里是晶胞对流), 这就减弱了外力. 外力的加强促使有序对流变为湍流和混沌 (参见第 1160 页 17.3). 在化学反应中也可以发生类似的现象. 描述这些现象的重要的方程例子有:

---

① “分岔” 是物理学和力学上的定名; 在数学上, bifurcation 定名为 “分歧”. ——译者注

---

a) 金兹堡-兰道 (Ginsburg-Landau, GL) 方程

$$\begin{array}{}\text{(9.151)}& u_t-u-\left(1+\mathrm{i}b\right)u_{xx}+\left(1+\mathrm{i}c\right){\left|u\right|}^{2}u=0,\end{array}$$

b) Kuramoto-Sivashinsky (KS) 方程 $u_t+u_{xx}+u_{xxxx}+u_x^2=0.\left(9.152\right)$

与无耗散的 KdV, NLS, SG 诸方程不同, 方程 (9.151) 和 (9.152) 是非线性耗散方程, 它们除了有时空周期解外, 还有时空无序 (混沌) 解. 时空模式或结构的出现是变成混沌的特征.

5. 耗散孤子

非保守系统中的孤 (孤立的) 波现象经常被称为耗散孤子 (dissipative solitons). 在保守系统中, 孤子通常形成一个至少具有一个连续改变参数的解族; 与保守系统不同, 可以在参数空间的单个点处发现耗散孤子, 在参数空间, 一方面在离差和非线性性之间, 另一方面在能量或粒子流和耗散之间形成一种平衡. 这个性质导致耗散孤子稳定性的一个特殊类型, 虽然它们不是可积波方程的解. 用复金兹堡-兰道方程是描述耗散孤子的方式之一. 耗散孤子出现在非线性光学空化、光学半导体放大器, 以及反应扩散系统中 (也见 [9.33]).

6. 非线性发展方程

发展方程 (evolution equations) 描述一个物理量随时间的发展. 它的例子有波方程 (参见第 777 页 9.2.3.2), 热方程 (参见第 779 页 9.2.3.3) 和薛定谔方程 (参见第 780 页 9.2.4.1). 发展方程的解被称为发展函数 (evolution functions).

与线性发展方程不同, 非线性发展方程 (9.148), (9.149) 和 (9.150) 包含非线性项 $u\partial u/\partial x,{\left|u\right|}^{2}u,\sin u$ 和 $u_x^2$ . 这些方程 (除了 (9.151) 是例外) 不含参数. 从物理学的观点来看, 非线性发展方程描述孤子 (弥散结构) 以及周期模式和非线性波 (耗散结构) 的结构形成.

9.2.5.2 科尔泰沃赫-德弗里斯方程 (KdV)

1. 出现 $\mathrm{KdV}$ 方程被用于下述一些情形的讨论中:

• 浅水中的表面波;
• 非线性格中的非谐振动;
• 等离子体物理学中的问题;
• 非线性电网.

2. 方程和解

发展函数 $u$ 的 $\mathrm{KdV}$ 方程是

$$\begin{array}{}\text{(9.153)}& u_t+6u{u}_x+u_{xxx}=0.\end{array}$$

它有孤子解

$$\begin{array}{}\text{(9.154)}& u\left(x,t\right)=\frac{v}{2{\cosh }^2\left[\frac{1}{2}\sqrt{v}\left(x-vt-\phi \right)\right]}.\end{array}$$

这个 $\mathrm{KdV}$ 孤子由两个无量纲参数 $v\left(v>0\right)$ 和 $\phi$ 唯一确定. 在图 9.22中选取了 $v=1$ . 一个典型的非线性效应是,孤子 $v$ 的速度决定了它的振幅和宽度: 具有较大振幅和较小宽度的孤子行进快于具有较小振幅和较大宽度的孤子 (较高的波行进快于较矮的波). 孤子的相 $\phi$ 描述孤子在时刻 $t=0$ 时最大值的位置.

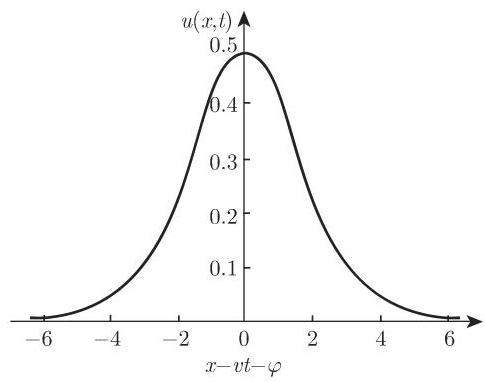
方程 (9.153) 也有一些 $N$ 孤子解. 这样一个 $N$ 孤子解可以用 1 孤子解的线性组合当 $t\to \pm \mathrm{\infty }$ 时渐近地表示:

$$\begin{array}{}\text{(9.155)}& u\left(x,t\right)\sim \sum _{n=1}^N{u}_n\left(x,t\right).\end{array}$$

这里每个发展函数 $u_n\left(x,t\right)$ 由一个速度 $v_n$ 和一个相 ${\phi }_n^{\pm }$ 所刻画. 在相互作用或碰撞前的初始相 ${\phi }_n^{-}$ 与碰撞后的最终相 ${\phi }_n^{+}$ 不同,而诸速度 $v_1,v_2,\cdots ,v_n$ 没有改变, 即, 这是一个弹性相互作用.

对于 $N=2,\left(9.153\right)$ 有一个 2 孤子解. 在有限时间内,它不能用一个线性叠加来表示,并且当 $k_n=\frac{1}{2}\sqrt{v_n}$ 和 ${\alpha }_n=\frac{1}{2}\sqrt{v_n}\left(x-v_{n}t-{\phi }_n\right)\left(n=1,2\right)$ 时,它有形式:

$$u\left(x,t\right)=8\frac{k_1^2{\mathrm{e}}^{{\alpha }_1}+k_2^2{\mathrm{e}}^{{\alpha }_2}+{(k_1-k_2)}^2{\mathrm{e}}^{({\alpha }_1+{\alpha }_2)}\left[2+\frac{1}{{(k_1+k_2)}^2}\left(k_1^2{\mathrm{e}}^{{\alpha }_1}+k_2^2{\mathrm{e}}^{{\alpha }_2}\right)\right]}{{[1+{\mathrm{e}}^{{\alpha }_1}+{\mathrm{e}}^{{\alpha }_2}+{\left(\frac{k_1-k_2}{k_1+k_2}\right)}^2{\mathrm{e}}^{({\alpha }_1+{\alpha }_2)}]}^2}.$$

(9.156)

方程 (9.156) 描述了当 $t\to -\mathrm{\infty }$ 时渐近地具有速度 $v_1=4k_1^2$ 和 $v_2=4k_2^2$ 的两个无相互作用的孤子,在它们相互作用后又变为两个没有相互作用的孤子,当 $t\to \mathrm{\infty }$ 时它们渐近地具有相同的速度.

非线性发展方程

$$\begin{array}{}\text{(9.157a)}& w_t+6{\left(w_x\right)}^2+w_{xxx}=0,\text{ 其中 }w=\frac{F_x}{F},\end{array}$$

有下述一些性质:

a) 对于 $F\left(x,t\right)=1+{\mathrm{e}}^{\alpha },\alpha =\frac{1}{2}\sqrt{v}\left(x-vt-\phi \right)$ .(9.157b)

它有一个孤子解, 并且

b) 对于 $F\left(x,t\right)=1+{\mathrm{e}}^{{\alpha }_1}+{\mathrm{e}}^{{\alpha }_2}+{\left(\frac{k_1-k_2}{k_1+k_2}\right)}^2{\mathrm{e}}^{{\alpha }_1+{\alpha }_2}$ .(9.157c)

它有一个 2 孤子解. 当 $2w_x=u$ 时,从方程 (9.157a) 即得 $\mathrm{KdV}$ 方程 (9.153). 方程 (9.156) 和由 (9.157c) 得到的表达式 $w$ 是非线性叠加的例子.

如果在(9.153)中以 $-6u{u}_x$ 代替 $+6u{u}_x$ ,那么(9.154)的右端必须乘以(-1). 在这个情形用记号反孤子 (antisoliton).

9.2.5.3 非线性薛定谔方程 (NLS)

1. 出现

NLS 方程出现在:

• 非线性光学中,其中折射率 $n$ 依赖于电场强度 $\overrightarrow{E}$ ,例如,对于克尔 (Kerr) 效应, 有 $n\left(\overrightarrow{E}\right)=n_0+n_2{\left|\overrightarrow{E}\right|}^2$ ,其中 $n_0$ 和 $n_2$ 是常数.

• 自引力 (self-gravitating) 圆盘的流体动力学中, 它使我们可以描述银河系旋臂.

2. 方程和解

发展函数 $u$ 的 NLS 方程及其解为

$$\begin{array}{}\text{(9.158)}& \mathrm{i}{u}_t+u_{xx}\pm 2{\left|u\right|}^{2}u=0,\end{array}$$$$\begin{array}{}\text{(9.159)}& u\left(x,t\right)=2\eta \frac{\exp \left(-\mathrm{i}\left[2\xi x+4\left({\xi }^2-{\eta }^2\right)t-\chi \right]\right)}{\cosh \left[2\eta \left(x+4\xi t-\phi \right)\right]},\end{array}$$

这里 $u\left(x,t\right)$ 是复的. NLS 孤子由 4 个无量纲的参数 $\eta ,\xi ,\phi$ 和 $\chi$ 所刻画. 波包的包络以速度 $v=-4\xi$ 行进; 波包的相速度是 $2\left({\eta }^2-{\xi }^2\right)/\xi$ .

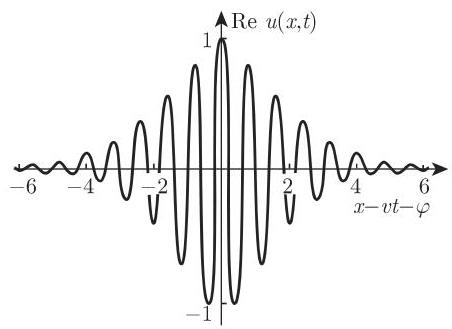
与 KdV 孤子 (9.154) 不同, NLS 孤子的振幅和速度可以互相独立地被选取. 图 9.23 展示了当 $\eta =1/2$ 和 $\xi =4$ 时 (9.159) 的实部.

(9.159) 形的解经常被称为光孤子 (light soliton), 它们解了 “+” 号情形的聚焦(focusing) NLS 方程 (9.158). 散焦 (defocusing) NLS 方程 ("-" 号情形) 给出孤子,在孤子位置处 ${\left|u\right|}^2$ 被简化为与常数背景 $\left|u\left(x\to \pm \mathrm{\infty }\right)\right|=\eta$ 的比较. 这样的暗孤子 (dark soliton) 有形式

$$\begin{array}{}\text{(9.160)}& u\left(x,t\right)=\left(\mathrm{i}\frac{v}{2}+\sqrt{{\eta }^2-\frac{v^2}{4}}\tanh \left[\sqrt{{\eta }^2-\frac{v^2}{4}}\left(x-vt\right)\right]\right)\cdot \exp \left[-\mathrm{i}\left(2{\eta }^{2}t+\chi \right)\right].\end{array}$$

它们依赖于 3 个参数 $\eta ,v$ 和 $\chi$ ,并在平凡 (平直) 相的背景下以速度 $v<2\eta$ 传播 (见 [9.41], [9.39]).

此外,通解有一个相梯度,这可以被解释为背景的速度 $v$ ,孤子以此速度在行进. 此时通解为

$$u\left(x,t\right)=\left(\mathrm{i}\frac{v}{2}+\sqrt{{\eta }^2-\frac{v^2}{4}}\right)\tanh \left[\sqrt{{\eta }^2-\frac{v^2}{4}}\left(x-vt-ct\right)\right]$$$$\begin{array}{}\text{(9.161)}& \times \exp \left[-\mathrm{i}\left(2{\eta }^{2}t+\chi -\frac{c}{2}x+\frac{c^2}{4}t\right)\right].\end{array}$$

除了这些指数位置的孤子波之外, NLS 方程还有一些周期解, 它们可以被解释为孤子的波包. 通过要求稳定, 并积分余下的常微分方程, 可以找到这样的解. 一般地, 这些解是椭圆雅可比函数 (参见第 997 页 14.6.2, 1.). 一些相关的解见 [9.34].

在有 $N$ 个相互作用的孤子的情形,可以通过 $4N$ 个任意选取的参数 ${\eta }_n,{\xi }_n,{\phi }_n$ , ${\chi }_n\left(n=1,2,\cdots ,N\right)$ 来刻画它们.

如果这些孤子有不同的速度,那么 $N$ -孤子解当 $t\to \pm \mathrm{\infty }$ 时渐近地分裂为形如 (9.159) 的 $N$ 个单独的孤子之和.

9.2.5.4 正弦戈登方程 (SG)

1. 出现

从空向非齐次二能级 (two-level) 量子力学系统的布洛赫 (Bloch) 方程得到 SG 方程. 它描述下述对象的传播:

• 在共振激光介质中的超短脉冲 (自感生透明);

• 在大曲面约瑟夫森接触, 即在两个超导体之间的隧道接触中的磁通量;

• 在超流氦-3 $\left({}^3\mathrm{He}\right)$ 中的自旋波.

SG 方程的孤子解可以用钟摆和弹簧的力学模型予以诠释. 发展函数连续地从零到某个常数 $c$ . SG 孤子经常被称为扭曲孤子 (kink solotin). 如果发展函数从常数值 $c$ 变化到零,则它描述一个所谓的反扭曲孤子 (antikink solotin). 可以用这种类型的解来描述区域结构的壁垒.

2. 方程和解

发展函数 $u$ 的 SG 方程是

$$\begin{array}{}\text{(9.162)}& u_{tt}-u_{xx}+\sin u=0.\end{array}$$

它有下述一些孤子解:

(1) 扭曲孤子

$$\begin{array}{}\text{(9.163)}& u\left(x,t\right)=4\arctan {\mathrm{e}}^{\gamma \left(x-x_0-vt\right)},\end{array}$$

其中 $\gamma =\frac{1}{\sqrt{1-v^2}},-1<v<+1$ .

图 9.24 给出了当 $v=1/2$ 时扭曲孤子 (9.163). 扭曲孤子由两个无量纲参数 $v$ 和 $x_0$ 所确定. 速度与振幅无关. 时间导数和位置导数是通常的局部化孤子:

$$\begin{array}{}\text{(9.164)}& -\frac{u_t}{v}=u_x=\frac{2\gamma }{\cosh \gamma \left(x-x_0-vt\right)}.\end{array}$$

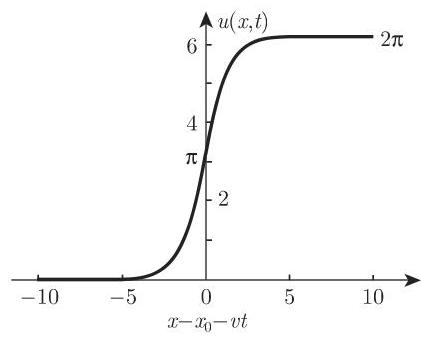
(2) 反扭曲孤子

$$\begin{array}{}\text{(9.165)}& u\left(x,t\right)=4\arctan {\mathrm{e}}^{-\gamma \left(x-x_0-vt\right)}.\end{array}$$

(3) 扭曲-反扭曲孤子 从(9.163,9.165),在 $v=0$ 时得到一个静态的扭曲-反扭曲孤子:

$$\begin{array}{}\text{(9.166)}& u\left(x,t\right)=4\arctan {\mathrm{e}}^{\pm \left(x-x_0\right)}.\end{array}$$

(9.162) 更多的解还有:

(4) 扭曲-扭曲碰撞

$$\begin{array}{}\text{(9.167)}& u\left(x,t\right)=4\arctan \left[v\frac{\sinh \gamma x}{\cosh \gamma vt}\right].\end{array}$$

(5) 扭曲-反扭曲碰撞

$$\begin{array}{}\text{(9.168)}& u\left(x,t\right)=4\arctan \left[\frac{1}{v}\frac{\sinh \gamma vt}{\cosh \gamma x}\right].\end{array}$$

(6) 双孤子或呼吸子孤子, 也称为扭曲-反扭曲偶极

$$\begin{array}{}\text{(9.169)}& u\left(x,t\right)=4\arctan \left[\frac{\sqrt{1-{\omega }^2}}{\omega }\frac{\sin \omega t}{\cosh \sqrt{1-{\omega }^2}x}\right].\end{array}$$

方程 (9.169) 表示一个定态波,其包络由频率 $\omega$ 所调制.

(7) 局部周期扭曲格

$$\begin{array}{}\text{(9.170a)}& u\left(x,t\right)=2\arcsin \left[\pm \mathrm{sn}\left(\frac{x-vt}{k\sqrt{1-v^2}},k\right)\right]+\pi .\end{array}$$

在波长 $\lambda$ 和格常数 $k$ 之间的关系为

$$\begin{array}{}\text{(9.170b)}& \lambda =4K\left(k\right)k\sqrt{1-v^2}.\end{array}$$

对于 $k=1$ ,即对于 $\lambda \to \mathrm{\infty }$ ,得到

$$\begin{array}{}\text{(9.170c)}& u\left(x,t\right)=4\arctan {\mathrm{e}}^{\pm \gamma \left(x-vt\right)},\end{array}$$

当 $x_0=0$ 时,它是扭曲孤子 (9.163),并且也是反扭曲孤子 (9.165).

注 $\mathrm{sn}x$ 是具有参数 $k$ 和 $1/4$ 周期 $K^{\text{①}}$ 的雅可比椭圆函数 (参见第 997 页14.6.2):

$$\begin{array}{}\text{(9.171a)}& \mathrm{sn}x=\sin \phi \left(x,k\right),\end{array}$$$$\begin{array}{}\text{(9.171b)}& x={\int }_0^{\sin \phi \left(x,k\right)}\frac{\mathrm{d}q}{\sqrt{\left(1-q^2\right)\left(1-k^2{q}^2\right)}},\end{array}$$$$\begin{array}{}\text{(9.171c)}& K\left(k\right)={\int }_0^{\pi /2}\frac{\mathrm{d}\mathrm{\Theta }}{\sqrt{1-k^2{\sin }^2\mathrm{\Theta }}}.\end{array}$$

从第 997 页的 (14.104a),由代换 $\sin \psi =q$ 即得方程 (9.171b). 完全椭圆积分的级数展开由第 683 页 8.2.5, 7., 方程 (8.104) 给出.

9.2.5.5 更多具有孤子解的非线性发展方程

1. 变形 $\mathrm{KdV}$ 方程

$$\begin{array}{}\text{(9.172)}& u_t\pm 6u^2{u}_x+u_{xxx}=0.\end{array}$$

更一般的方程 (9.173) 有孤子解 (9.174).

$$\begin{array}{}\text{(9.173)}& u_t+u^p{u}_x+u_{xxx}=0,\end{array}$$$$\begin{array}{}\text{(9.174)}& u\left(x,t\right)={\left[\frac{\frac{1}{2}\left|v\right|\left(p+1\right)\left(p+2\right)}{{\cosh }^2\left(\frac{1}{2}p\sqrt{\left|v\right|}\left(x-vt-\phi \right)\right)}\right]}^{\frac{1}{p}}.\end{array}$$

---

① 即 $4K$ 是 $\mathrm{sn}x$ 的一个周期. - 译者注

---

2. 双曲正弦戈登方程

$$\begin{array}{}\text{(9.175)}& u_{tt}-u_{xx}+\sinh u=0.\end{array}$$

3. 布西内斯克 (Boussinesq) 方程

$$\begin{array}{}\text{(9.176)}& u_{xx}-u_{tt}+{\left(u^2\right)}_{xx}+u_{xxxx}=0.\end{array}$$

这个方程出现在非线性电网络作为电荷-电压关系的一种连续逼近的描述中.

4. 广田 (Hirota) 方程

$$\begin{array}{}\text{(9.177)}& u_t+\mathrm{i}3\alpha {\left|u\right|}^2{u}_x+\beta u_{xx}+\mathrm{i}\sigma u_{xxx}+\delta {\left|u\right|}^{2}u=0,\alpha \beta =\sigma \delta .\end{array}$$

5. 伯格斯 (Burgers) 方程

$$\begin{array}{}\text{(9.178)}& u_t-u_{xx}+u{u}_x=0.\end{array}$$

在湍流模型中出现这个方程. 用霍普夫-科尔 (Hopf-Cole) 变换可以将其变为扩散方程, 即变为一个线性微分方程.

6. Kadomzev-Pedviashwili 方程

方程

$$\begin{array}{}\text{(9.179a)}& {(u_t+6u{u}_x+u_{xxx})}_x=u_{yy}\end{array}$$

有孤子解

$$\begin{array}{}\text{(9.179b)}& u\left(x,y,t\right)=2\frac{{\partial }^2}{\partial x^2}\ln \left[\frac{1}{k^2}+{|x+\mathrm{i}ky-3k^{2}t|}^2\right].\end{array}$$

方程 (9.179a) 是具有较多自变量, 例如, 两个空间变量的孤子方程的例子.

注 本手册德文版的只读光碟存储器 (CD-ROM) 包含了更多的非线性发展方程. 再者, 展示了解线性偏微分方程的傅里叶变换和逆散射理论的一些应用.