18.2.1 问题的提法、理论基础

18.2.1.1 问题的提法

1. 非线性优化问题

非线性优化问题的一般形式是

$$\begin{array}{}\text{(18.32a)}& f\left(\underset{―}{\mathbf{x}}\right)=min!,\underset{―}{\mathbf{x}}\in {\mathbb{R}}^n\text{满足如下约束条件:}\end{array}$$$$\begin{array}{}\text{(18.32b)}& g_i\left(\underset{―}{\mathbf{x}}\right)\le 0,i\in I=\{1,\cdots ,m\},h_j\left(\underset{―}{\mathbf{x}}\right)=0,j\in J=\{1,\cdots ,r\},\end{array}$$

这里函数 $f,g_i,h_j$ 中至少有一个是非线性的. 可行解集是

$$\begin{array}{}\text{(18.33)}& M=\left\{\underset{―}{\mathbf{x}}\in {\mathbb{R}}^n:g_i\left(\underset{―}{\mathbf{x}}\right)\le 0,i\in I,h_j\left(\underset{―}{\mathbf{x}}\right)=0,j\in J\right\}.\end{array}$$

问题是要确定极小点.

2. 极小点

点 ${\underset{―}{\mathbf{x}}}^{\ast }\in M$ 称作全局极小点,是指它满足 $f\left({\underset{―}{\mathbf{x}}}^{\ast }\right)\le f\left(\underset{―}{\mathbf{x}}\right),\mathrm{\forall }\underset{―}{\mathbf{x}}\in M$ . 如果这个关系仅对于 ${\underset{―}{x}}^{\ast }$ 的某个邻域 $U$ 中的点 $\underset{―}{x}$ 成立,则 ${\underset{―}{x}}^{\ast }$ 称作局部极小点. 由于等式约束 $h_j\left(\underset{―}{\mathbf{x}}\right)=0$ 可以用两个不等式约束表达:

$$\begin{array}{}\text{(18.34)}& -h_j\left(\underset{―}{\mathbf{x}}\right)\le 0,h_j\left(\underset{―}{\mathbf{x}}\right)\le 0,\end{array}$$

故可以假定集合 $J$ 是空的, $J=\varnothing$ .

18.2.1.2 最优性条件

1. 特殊方向

a) 可行方向锥 $\underset{―}{x}\in M$ 处的可行方向锥定义为

$$\begin{array}{}\text{(18.35)}& Z\left(\underset{―}{\mathbf{x}}\right)=\left\{\underset{―}{\mathbf{d}}\in {\mathbb{R}}^n:\mathrm{\exists }\overline{\alpha }>0\text{ 使得 }\underset{―}{\mathbf{x}}+\alpha \underset{―}{\mathbf{d}}\in M,0\le \alpha \le \overline{\alpha }\right\},\underset{―}{\mathbf{x}}\in M,\end{array}$$

其中 $\underset{―}{d}$ 表示方向. 如果 $\underset{―}{d}\in Z\left(\underset{―}{x}\right)$ ,那么射线 $\underset{―}{x}+\alpha \underset{―}{d}$ 上的每个点当 $\alpha$ 充分小时都属于 $M$ .

b) 下降方向 点 $\underset{―}{x}$ 处的下降方向是指一向量 $\underset{―}{d}\in \mathbb{R}$ ,存在 $\overline{\alpha }>0$ 使得

$$\begin{array}{}\text{(18.36)}& f\left(\underset{―}{\mathbf{x}}+\alpha \underset{―}{\mathbf{d}}\right)<f\left(\underset{―}{\mathbf{x}}\right),\mathrm{\forall }\alpha \in \left(0,\overline{\alpha }\right).\end{array}$$

显然在极小点不存在可行下降方向. 如果 $f$ 可微,则当 $\mathrm{\nabla }f{\left(\underset{―}{\mathbf{x}}\right)}^{\mathrm{T}}\underset{―}{\mathbf{d}}<0$ 时, $\underset{―}{\mathbf{d}}$ 是下降方向. 在这里 $\mathrm{\nabla }$ 表示梯度算子,故 $\mathrm{\nabla }f\left(\underset{―}{x}\right)$ 表示标量值函数 $f$ 在 $\underset{―}{x}$ 处的梯度.

2. 最优性必要条件

如果 $f$ 可微并且 ${\underset{―}{x}}^{\ast }$ 是一局部极小点,那么

$$\begin{array}{}\text{(18.37a)}& \mathrm{\nabla }f{\left({\underset{―}{\mathbf{x}}}^{\ast }\right)}^{\mathrm{T}}\underset{―}{\mathbf{d}}\ge 0,\mathrm{\forall }\underset{―}{\mathbf{d}}\in \overline{Z}\left({\underset{―}{\mathbf{x}}}^{\ast }\right).\end{array}$$

特别地,若 ${\underset{―}{\mathbf{x}}}^{\ast }$ 是 $M$ 的内点,那么

$$\begin{array}{}\text{(18.37b)}& \mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^{\ast }\right)=\underset{―}{\mathbf{0}}.\end{array}$$

3. 拉格朗日函数和鞍点

最优性条件 (18.37a, 18.37b) 应该翻译成包含约束的更实用的形式. 根据对于具有等式约束问题的拉格朗日乘子法 (参见第 611 页 6.2.5.6), 构造所谓的拉格朗日函数:

$$\begin{array}{}\text{(18.38)}& L\left(\underset{―}{\mathbf{x}},\underset{―}{\mathbf{u}}\right)=f\left(\underset{―}{\mathbf{x}}\right)+\sum _{i=1}^m{u}_i{g}_i\left(\underset{―}{\mathbf{x}}\right)=f\left(\underset{―}{\mathbf{x}}\right)+{\underset{―}{\mathbf{u}}}^{\mathrm{T}}g\left(\underset{―}{\mathbf{x}}\right),\underset{―}{\mathbf{x}}\in {\mathbb{R}}^n,\underset{―}{\mathbf{u}}\in {\mathbb{R}}_{+}^m.\end{array}$$

点 $\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{u}}}^{\ast }\right)\in {\mathbb{R}}^n\times {\mathbb{R}}_{+}^m$ 称作 $L$ 的鞍点,是指

$$\begin{array}{}\text{(18.39)}& L\left({\underset{―}{\mathbf{x}}}^{\ast },\underset{―}{\mathbf{u}}\right)\le L\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{u}}}^{\ast }\right)\le L\left(\underset{―}{\mathbf{x}},{\underset{―}{\mathbf{u}}}^{\ast }\right),\mathrm{\forall }\underset{―}{\mathbf{x}}\in {\mathbb{R}}^n,\underset{―}{\mathbf{u}}\in {\mathbb{R}}_{+}^m.\end{array}$$

4. 全局库恩-塔克条件

如果存在 ${\underset{―}{\mathbf{u}}}^{\ast }\in {\mathbb{R}}_{+}^m$ ,即 ${\underset{―}{\mathbf{u}}}^{\ast }\ge \underset{―}{\mathbf{0}}$ 使得 $\left({\underset{―}{\mathbf{x}}}^{\ast },{\underset{―}{\mathbf{u}}}^{\ast }\right)$ 是 $L$ 的鞍点,则点 ${\underset{―}{\mathbf{x}}}^{\ast }$ 满足全局库恩-塔克条件. 至于库恩-塔克条件的证明, 参见第 893 页 12.5.6.

5. 最优性充分条件

如果点 $\left({\underset{―}{x}}^{\ast },{\underset{―}{u}}^{\ast }\right)\in {\mathbb{R}}^n\times {\mathbb{R}}_{+}^m$ 是 $L$ 的鞍点,那么 ${\underset{―}{x}}^{\ast }$ 是(18.32a,18.32b)的全局极小点. 如果函数 $f$ 和 $g_i$ 可微,则可以推导出局部最优性条件.

6. 局部库恩-塔克条件

如果存在数 $u_i\ge 0,i\in I_0\left({\underset{―}{\mathbf{x}}}^{\ast }\right)$ 使得

$$\begin{array}{}\text{(18.40a)}& -\mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^{\ast }\right)=\sum _{i\in I_0\left({\underset{―}{\mathbf{x}}}^{\ast }\right)}{u}_i\mathrm{\nabla }{g}_i\left({\underset{―}{\mathbf{x}}}^{\ast }\right),\end{array}$$

其中

$$\begin{array}{}\text{(18.40b)}& I_0\left(\underset{―}{\mathbf{x}}\right)=\left\{i\in \{1,\cdots ,m\}:g_i\left(\underset{―}{\mathbf{x}}\right)=0\right\}\end{array}$$

是 $\underset{―}{x}$ 处主动约束的标号集. ${\underset{―}{x}}^{\ast }$ 也称作库恩-塔克平稳点.

这就意味着在几何上,如果负梯度 $-\mathrm{\nabla }f\left({\underset{―}{x}}^{\ast }\right)$ 位于由 ${\underset{―}{x}}^{\ast }$ 处主动约束 (即 $i\in$ $I_0\left({\underset{―}{\mathbf{x}}}^{\ast }\right))$ 对应的诸梯度 $\mathrm{\nabla }{g}_i\left({\underset{―}{\mathbf{x}}}^{\ast }\right)$ 所张成的锥中 (图 18.5),则 ${\underset{―}{\mathbf{x}}}^{\ast }$ 满足库恩-塔克条件.

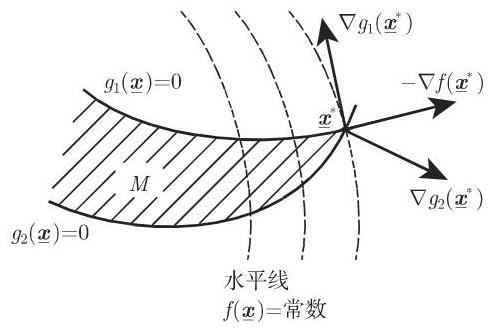
局部库恩-塔克条件 (18.40a, 18.40b) 的如下等价表述也是经常使用的:如果存在 ${\underset{―}{\mathbf{u}}}^{\ast }\in {\mathbb{R}}_{+}^m$ 使得

$$\begin{array}{}\text{(18.41a)}& g\left({\underset{―}{\mathbf{u}}}^{\ast }\right)\le 0,\end{array}$$$$\begin{array}{}\text{(18.41b)}& u_i{g}_i\left({\underset{―}{\mathbf{u}}}^{\ast }\right)=0,i=1,\cdots ,m,\end{array}$$$$\begin{array}{}\text{(18.41c)}& \mathrm{\nabla }f\left({\underset{―}{\mathbf{x}}}^{\ast }\right)+\sum _{i=1}^m{u}_i\mathrm{\nabla }{g}_i\left({\underset{―}{\mathbf{x}}}^{\ast }\right)=0,\end{array}$$

那么 ${\underset{―}{\mathbf{x}}}^{\ast }\in {\mathbb{R}}^n$ 满足局部库恩-塔克条件.

7. 最优性必要条件和库恩-塔克条件

如果 ${\underset{―}{x}}^{\ast }\in M$ 是(18.32a,18.32b)的局部极小点,并且可行集在 ${\underset{―}{x}}^{\ast }$ 处满足正则性条件: $\mathrm{\exists }\underset{―}{\mathbf{d}}\in {\mathbb{R}}^n$ 使得 $\mathrm{\nabla }{g}_i{\left({\underset{―}{\mathbf{x}}}^{\ast }\right)}^{\mathrm{T}}\underset{―}{\mathbf{d}}<0,\mathrm{\forall }i\in I_0\left({\underset{―}{\mathbf{x}}}^{\ast }\right)$ ,那么 ${\underset{―}{\mathbf{x}}}^{\ast }$ 满足库恩-塔克条件.

18.2.1.3 优化中的对偶性

1. 对偶问题

采用相关的拉格朗日函数 (18.32a, 18.32b), 构造极大问题, 即 (18.32a, 18.32b) 的所谓对偶问题:

$$\begin{array}{}\text{(18.42a)}& L\left(\underset{―}{\mathbf{x}},\underset{―}{\mathbf{u}}\right)=max!,\left(\underset{―}{\mathbf{x}},\underset{―}{\mathbf{u}}\right)\in M^{\ast },\end{array}$$

其中

$$\begin{array}{}\text{(18.42b)}& M^{\ast }=\left\{\left(\underset{―}{\mathbf{x}},\underset{―}{\mathbf{u}}\right)\in {\mathbb{R}}^n\times {\mathbb{R}}_{+}^m:L\left(\underset{―}{\mathbf{x}},\underset{―}{\mathbf{u}}\right)=\underset{\underset{―}{\mathbf{z}}\in {\mathbb{R}}^n}{min}L\left(\underset{―}{\mathbf{z}},\underset{―}{\mathbf{u}}\right)\right\}.\end{array}$$

2. 对偶性定理

如果 ${\underset{―}{\mathbf{x}}}_1\in M$ ,并且 $\left({\underset{―}{\mathbf{x}}}_2,{\underset{―}{\mathbf{u}}}_2\right)\in M^{\ast }$ ,那么

**a) $L(\ast \ast {\underset{―}{\mathbf{x}}}_2,{\underset{―}{\mathbf{u}}}_2)\le f\left({\underset{―}{\mathbf{x}}}_1\right)$ .

b) 如果 $L\left({\underset{―}{\mathbf{x}}}_2,{\underset{―}{\mathbf{u}}}_2\right)=f\left({\underset{―}{\mathbf{x}}}_1\right)$ ,则 ${\underset{―}{\mathbf{x}}}_1$ 是(18.32a,18.32b)的极小点,而 $\left({\underset{―}{\mathbf{x}}}_2,{\underset{―}{\mathbf{u}}}_2\right)$ 是(18.42a,18.42b)的极大点.