16.2.2 随机变量、分布函数

要应用概率论中的分析方法, 变量和函数的概念是很有必要的.

16.2.2.1 随机变量

基本事件集可用随机变量 $X$ 来描述. 随机变量 $X$ 可视为在实数子集 $R$ 中随机取值 $x$ 的量.

若 $R$ 包含有限或可数多个不同的值,则称 $X$ 为离散随机变量. 对于连续随机变量, $R$ 可能是全体实数或包含一些子区间. 随机变量的精确定义见第 1062 页 16.2.2.2, 2., 也存在混合随机变量.

$◼\mathbf{A}$: 在第 1057 页例A中,令基本事件 $A_{11},A_{12},A_{21},A_{22}$ 分别取值1,2,3,4,则定义了一个离散随机变量 $X$ .

$◼\mathbf{B}$: 随机选取的灯泡寿命 $T$ 是一个连续随机变量. 若寿命 $T$ 等于 $t$ ,则发生了基本事件 $T=t$ .

16.2.2.2 分布函数

1. 分布函数及其性质

随机变量 $X$ 的分布可由其分布函数

$$\begin{array}{}\text{(16.44)}& F\left(x\right)=P\left(X\le x\right),-\mathrm{\infty }\le x\le \mathrm{\infty }\end{array}$$

给出,它决定取值于 $(-\mathrm{\infty },x]$ 的随机变量 $X$ 的概率,其定义域是全体实数. 分布函数具有下述性质:

(1) $F\left(-\mathrm{\infty }\right)=0,F\left(+\mathrm{\infty }\right)=1$ .

(2) $F\left(x\right)$ 是关于 $x$ 的非减函数.

(3) $F\left(x\right)$ 是右连续的.

注 (1) 由定义可推出 $P\left(X=a\right)=F\left(a\right)-\underset{x\to a-0}{lim}F\left(x\right)$ .

(2)文献中也经常使用 $F\left(x\right)=P\left(X<x\right)$ 作为定义. 此时,

$$P\left(X=a\right)=\underset{x\to a+0}{lim}F\left(x\right)-F\left(a\right).$$

2. 离散随机变量和连续随机变量的分布函数

a) 离散随机变量 若离散随机变量 $X$ 的取值为 $x_i\left(i=1,2,\cdots \right)$ ,对应的概率为 $P\left(X=x_i\right)=p_i\left(i=1,2,\cdots \right)$ ,则其分布函数为

$$\begin{array}{}\text{(16.45)}& F\left(x\right)=\sum _{x_i\le x}{p}_i.\end{array}$$

b) 连续随机变量 若存在非负函数 $f\left(x\right)$ ,使得对任何可能在其上考虑积分的区域 $S$ ,概率 $P\left(X\in S\right)$ 可表示为 $P\left(X\in S\right)={\int }_{S}f\left(x\right)\mathrm{d}x$ ,则称随机变量 $X$ 是连续的. 函数 $f\left(x\right)$ 即所谓的密度函数. 连续随机变量在任意给定值 $x_i$ 处的概率为 0, 因此我们只需要考虑 $X$ 取值于有限区间 $\left[a,b\right]$ 的概率:

$$\begin{array}{}\text{(16.46)}& P\left(a\le X\le b\right)={\int }_a^{b}f\left(t\right)\mathrm{d}t.\end{array}$$

连续随机变量有处处连续的分布函数:

$$\begin{array}{}\text{(16.47)}& F\left(x\right)=P\left(X\le x\right)={\int }_{-\mathrm{\infty }}^{x}f\left(t\right)\mathrm{d}t.\end{array}$$

在 $f\left(x\right)$ 连续的点处有 $F^{\prime }\left(x\right)=f\left(x\right)$ 成立.

注 当与积分上限不混淆时,通常用 $x$ 代替 $t$ 表示积分变量.

3. 概率的面积解释、分位数

通过引入 (16.47) 中的分布函数和密度函数,概率 $P\left(X\le x\right)=F\left(x\right)$ 可表示为区间 $-\mathrm{\infty }<t\le x$ 上密度函数 $f\left(t\right)$ 和 $x$ 轴之间的图形面积 (图 16.1(a)).

通常给定一个概率值 $\alpha$ (经常以 $\mathrm{\%}$ 表示),如果

$$\begin{array}{}\text{(16.48)}& P\left(X>x\right)=\alpha \end{array}$$

成立,对应的横坐标值 $x=x_{\alpha }$ 称为分位数或 $\alpha$ 分位数(图 16.1(b)). 这说明密度函数 $f\left(t\right)$ 下方、 $x_{\alpha }$ 右侧的图形面积等于 $\alpha$ .

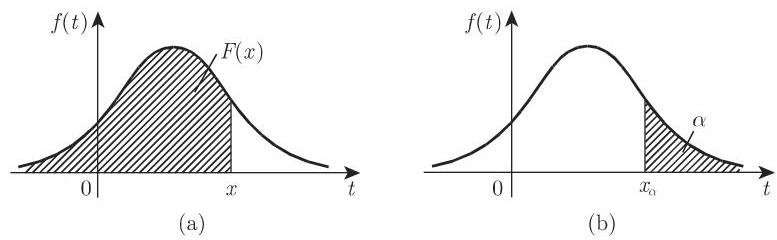
注 文献中也把 $x_{\alpha }$ 左侧的图形面积作为分位数的定义. 在数理统计学中,对于一些较小的 $\alpha$ 值,如 $\alpha =5\mathrm{\%}$ 或 $\alpha =1\mathrm{\%}$ ,也作为第一类显著性水平或犯第一类错误的概率. 实践中一些重要分布的常用分位数已列表给出 (参见第 1456 页表 21.16 至第 1463 页表 21.20).

16.2.2.3 期望和方差、切比雪夫不等式

在粗糙描述随机变量 $X$ 的分布时,大多用到的参数是 $\mu$ 表示的期望和 ${\sigma }^2$ 表示的方差. 若用力学术语来解释,期望指由密度函数曲线 $f\left(x\right)$ 和 $x$ 轴围成的曲面重心的横坐标. 方差是随机变量 $X$ 偏离其期望 $\mu$ 的一个度量.

1. 期望

若 $g\left(X\right)$ 是随机变量 $X$ 的函数,则 $g\left(X\right)$ 也是随机变量,其期望值或期望的定义为 a) 离散情形 $E\left(g\left(X\right)\right)=\sum _{k}g\left(x_k\right)p_k$ ,若级数 $\sum _{k=1}^{\mathrm{\infty }}\left|g\left(x_k\right)\right|p_k$ 存在.(16.49a)

b) 连续情形 $E\left(g\left(X\right)\right)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}g\left(x\right)f\left(x\right)\mathrm{d}x$ ,若 ${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\left|g\left(x\right)\right|f\left(x\right)\mathrm{d}x$ 存在.(16.49b)

当 $g\left(X\right)=X$ 时,随机变量的期望可定义为

$$\begin{array}{}\text{(16.50a)}& {\mu }_X=E\left(X\right)=\sum _k{x}_k{p}_k\text{ 或 }{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}xf\left(x\right)\mathrm{d}x,\end{array}$$

只要对应的级数或积分绝对收敛. 根据 (16.49a, 16.49b),

$$\begin{array}{}\text{(16.50b)}& E\left(aX+b\right)=a{\mu }_X+b\left(a,b\text{ 是常数 }\right)\end{array}$$

也成立. 当然,随机变量 $g\left(X\right)$ 的期望也可能不存在.

2. $n$ 阶矩

我们进一步介绍:

a) $n$ 阶矩 $E\left(X^n\right)$ .(16.51a)

b) $n$ 阶中心矩 $E\left({(X-{\mu }_X)}^n\right)$ .(16.51b)

3. 方差和标准差

特别地, 2 阶中心矩称为方差或离差:

$$\begin{array}{}\text{(16.52)}& E\left({(X-{\mu }_X)}^2\right)=D^2\left(X\right)={\sigma }_X^2=\{\begin{array}{l}\sum _k{(x_k-{\mu }_X)}^2{p}_k\\ \text{ 或 }\\ {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{(x-{\mu }_X)}^{2}f\left(x\right)\mathrm{d}x,\end{array}\end{array}$$

若公式中的期望存在. ${\sigma }_X$ 称为标准差. 下述关系式成立:

$$\begin{array}{}\text{(16.53)}& D^2\left(X\right)={\sigma }_X^2=E\left(X^2\right)-{\mu }_X^2,D^2\left(aX+b\right)=a^2{D}^2\left(X\right).\end{array}$$

4. 加权平均和算术平均

在离散情形下,期望显然是数值 $x_1,\cdots ,x_n$ 和概率 $p_k\left(k=1,\cdots ,n\right)$ 作为权重的加权平均

$$\begin{array}{}\text{(16.54)}& E\left(X\right)=p_1{x}_1+\cdots +p_n{x}_n.\end{array}$$

均匀分布的概率是 $p_1=p_2=\cdots =p_n=1/n,E\left(X\right)$ 是 $x_k$ 的算术平均:

$$\begin{array}{}\text{(16.55)}& E\left(X\right)=\frac{x_1+x_2+\cdots +x_n}{n}.\end{array}$$

在连续情形下,在有限区间 $\left[a,b\right]$ 上连续均匀分布的密度函数是

$$\begin{array}{}\text{(16.56)}& f\left(x\right)=\{\begin{array}{ll}\frac{1}{b-a},& a\le x\le b,\\ 0,& \text{ 其他. }\end{array}\end{array}$$

由此得到

$$\begin{array}{}\text{(16.57)}& E\left(X\right)=\frac{1}{b-a}{\int }_a^{b}x\mathrm{d}x=\frac{a+b}{2},{\sigma }_X^2=\frac{{(b-a)}^2}{12}.\end{array}$$

5. 切比雪夫不等式

如果随机变量 $X$ 的期望为 $\mu$ ,标准差为 $\sigma$ ,则对任意 $\lambda >0$ ,有切比雪夫不等式 (参见第 39 页 1.4.2.10):

$$\begin{array}{}\text{(16.58)}& P\left(\left|X-\mu \right|\ge \lambda \sigma \right)\le \frac{1}{{\lambda }^2}.\end{array}$$

也就是说,随机变量 $X$ 与期望 $\mu$ 的距离不太可能超过标准差的 $\lambda$ 倍 ( $\lambda$ 很大).

16.2.2.4 多维随机变量

如果基本事件是指 $n$ 个随机变量 $X_1,\cdots ,X_n$ 取 $n$ 个实值 $x_1,\cdots ,x_n$ ,则我们定义了一个随机向量 $\underset{―}{\mathbf{X}}=\left(X_1,X_2,\cdots ,X_n\right)$ (也可参见第 1084 页,16.3.1.1,4.). 其相应的分布函数可定义为

$$\begin{array}{}\text{(16.59)}& F\left(x_1,\cdots ,x_n\right)=P\left(X_1\le x_1,\cdots ,X_n\le x_n\right).\end{array}$$

若存在函数 $f\left(t_1,\cdots ,t_n\right)$ 使得

$$\begin{array}{}\text{(16.60)}& F\left(x_1,\cdots ,x_n\right)={\int }_{-\mathrm{\infty }}^{x_1}\cdots {\int }_{-\mathrm{\infty }}^{x_n}f\left(t_1,\cdots ,t_n\right)\mathrm{d}{t}_1\cdots \mathrm{d}{t}_n\end{array}$$

成立,则随机向量称为连续的. 函数 $f\left(t_1,\cdots ,t_n\right)$ 称为密度函数,它是非负的. 当 $x_1,\cdots ,x_n$ 中的一些变量趋于无穷时,则得到所谓的边际分布. 关于边际分布的深入研究和例子可参考相关文献.

随机变量 $X_1,\cdots ,X_n$ 是独立随机变量,如果

$$\begin{array}{}\text{(16.61)}& F\left(x_1,\cdots ,x_n\right)=F_1\left(x_1\right)F_2\left(x_2\right)\cdots F_n\left(x_n\right),\end{array}$$$$f\left(x_1,\cdots ,x_n\right)=f_1\left(x_1\right)f_2\left(x_2\right)\cdots f_n\left(x_n\right).$$