1.3.5 折旧

1.3.5.1 折旧法

折旧这一术语多数用来指由于陈旧过时或物质因素, 资产的服务潜能在某年内有所下降. 折旧是把报告年度开始时的原值 (原价)减少到年末残值的一种方法.

使用下述概念:

• $A$ 为折旧基数,

• $N$ 为有效期限 (以年给出),

• $R_n$ 为 $n$ 年后的残值 $\left(n\le N\right)$ ,

• $a_n\left(n=1,2,\cdots ,N\right)$ 为第 $n$ 年的折旧率.

折旧法不同于其他基于分期偿还率的方法:

• 直线法, 即年率相等,

• 递减分摊法, 即年率递减.

1.3.5.2 直线法

年折旧是常数,即对分期偿还率 $a_n$ 和 $n$ 年后的剩余值 $R_n$ ,有

$$\begin{array}{}\text{(1.88)}& a_n=\frac{A-R_N}{N}=a,\end{array}$$$$\begin{array}{}\text{(1.89)}& R_n=A-n\frac{A-R_N}{N}\left(n=1,2,\cdots ,N\right).\end{array}$$

用 $R_N=0$ 进行替换,则 $N$ 年后给定事物的价值减小到 0,即完全折旧.

一台机器的购买价是 $A=\text{€}50000,5$ 年内将折价到 $R_5=\text{€}10000$ . 根据 (1.88) 和 (1.89) 式, 线性折旧生成下述分摊表, 表格显示, 对于实际原价的累积折旧率逐渐增大.

	折旧基数	折旧额	残值	对折旧基数的 累积折旧率 (%)
1 年	50000	8000	42000	16.0
2 年	42000	8000	34000	19.0
3 年	34000	8000	26000	23.5
4 年	26000	8000	18000	30.8
5 年	18000	8000	10000	44.4

1.3.5.3 余额算术递减折旧法

这种情况下,折旧不是常数. 它以相同数量 $d$ (即所谓倍数) 逐年减小. 第 $n$ 年的折旧满足:

$$\begin{array}{}\text{(1.90)}& a_n=a_1-\left(n-1\right)d\left(n=2,3,\cdots ,N+1;a_1\text{ 和 }d\text{ 已知 }\right).\end{array}$$

对于等式 $A-R_N=\sum _{n=1}^N{a}_n$ ,由以前的方程可推出:

$$\begin{array}{}\text{(1.91)}& d=\frac{2\left[N{a}_1-\left(A-R_N\right)\right]}{N\left(N-1\right)}.\end{array}$$

当 $d=0$ 时,即直线折旧的特殊情形. 若 $d>0$ ,由 (1.91) 式可推出

$$\begin{array}{}\text{(1.92)}& a_1>\frac{A-R_N}{N}=a,\end{array}$$

其中, $a$ 是直线折旧的折旧率. 余额算术递减折旧法的第一个折旧率 $a_1$ 必须满足下述不等式:

$$\begin{array}{}\text{(1.93)}& \frac{A-R_N}{N}<a_1<2\frac{A-R_N}{N}.\end{array}$$

$◼$ 购买价为€50000 的机器在 5 年内按照算术递减折旧法折价到€10000. 第一年应折旧€15000. 根据给定公式可算出下述折旧表, 表格显示, 除了最后一个数值, 折旧率大致相等.

	折旧基数	折旧额	残值	对折旧基数 的折旧率 (%)
1 年	50000	15000	35000	30.0
2 年	35000	11500	23500	32.9
3 年	23500	8000	15500	34.0
4 年	15500	4500	11000	29.0
5 年	11000	1000	10000	9.1

1.3.5.4 余额数字递减折旧法

数字折旧是算术递减折旧的特殊情况,此时需要最后的折旧率 $a_N$ 等于倍数 $d$ . 由 $a_N=d$ 可推出

$$\begin{array}{}\text{(1.94a)}& d=\frac{2\left(A-R_N\right)}{N\left(N+1\right)}\end{array}$$$$\begin{array}{}\text{(1.94b)}& a_1=Nd{a}_2=\left(N-1\right)d,\cdots ,a_N=d.\end{array}$$

$◼$ 机器的购买价是 $A=\text{€}50000,5$ 年内按照数字折旧法折价到 $R_5=\text{€}10000$ .

根据给定公式可算出下述折旧表, 表格显示, 折旧率大致相等.

	折旧基数	折旧额	残值	对折旧基数 的折旧率 (%)
1 年	50000	$a_1=5d=13335$	36665	26.7
2 年	36665	$a_2=4d=10668$	25997	29.1
3 年	25997	$a_3=3d=8001$	17996	30.8
4 年	17996	$a_4=2d=5334$	12662	29.6
5 年	12662	$a_5=d=2667$	9995	21.1

1.3.5.5 余额几何递减折旧法

对于几何递减折旧法,每年折旧实际价格的 $p\mathrm{\%}.n$ 年后的残值 $R_n$ 为

$$\begin{array}{}\text{(1.95)}& R_n=A{(1-\frac{p}{100})}^n\left(n=1,2,\cdots \right).\end{array}$$

$A$ (购置成本) 通常是已知的. 资产的有效期限是 $N$ 年. 对于数量 $R_N,p$ 和 $N$ , 若已知两个, 则由 (1.95) 式可计算出第三个.

$◼\mathbf{A}$:购买价为€50000 的机器以 10% 的年率几何折旧,几年后其值将首次降至€10000 以下? 根据 (1.95) 式可得

$$N=\frac{\ln \left(\frac{10000}{50000}\right)}{\ln \left(1-0.1\right)}=15.27\text{ (年). }$$

$◼\mathbf{B}$: 购买价 $A=\text{€}1000$ ,对于 $n=1,2,\cdots ,10$ 年,残值 $R_n$ 分别按下述方式折旧: ①直线, ②算术递减, ③ 几何递减, 结果见图 1.4.

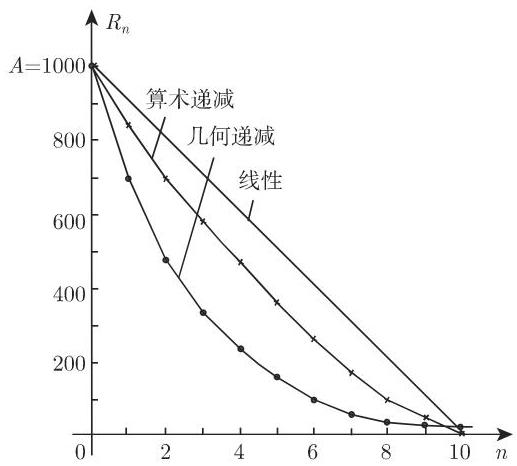
1.3.5.6 不同类型分期折旧的折旧法

在几何递减折旧情形,对于有限的 $n$ ,残值不能等于 0,因此,经过一定时间后, 如经过 $m$ 年,几何递减折旧变换成直线折旧是合理的. $m$ 是待确定的量,从这一时刻起, 几何递减折旧率小于直线折旧率. 根据这一要求, 可推出

$$\begin{array}{}\text{(1.96)}& m>N-\frac{100}{p}.\end{array}$$

此时, $m$ 是几何递减折旧的最后一年, $N$ 是当残值为 0 时,线性折旧的最后一年.

$◼$ 购买价为€50000 的机器,欲在 15 年内折旧到 0,前 $m$ 年以残值的 $14\mathrm{\%}$ ,按照几何递减方式折旧,然后以直线法折旧. 由 (1.96) 式可推出 $m>15-\frac{100}{14}=7.76$ ,即 $m=8$ 年后,变换成直线折旧比较合理.