8.5.3 一般类型的曲面积分

8.5.3.1 一般类型的曲面积分的概念

若 $P\left(x,y,z\right),Q\left(x,y,z\right),R\left(x,y,z\right)$ 为定义在一连通区域上的三个三元函数, $S$ 为该区域内的有向曲面, 在三个坐标面上投影的第二类积分之和称为一般类型的曲

面积分:

$$\begin{array}{}\text{(8.161)}& {\int }_S\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right)={\int }_{S}P\mathrm{d}y\mathrm{d}z+{\int }_{S}Q\mathrm{d}z\mathrm{d}x+{\int }_{S}R\mathrm{d}x\mathrm{d}y.\end{array}$$

该公式可化为二重积分:

$${\int }_S\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right)={\int }_{\mathrm{\Delta }}\left[P\frac{D\left(y,z\right)}{D\left(u,v\right)}+Q\frac{D\left(z,x\right)}{D\left(u,v\right)}+R\frac{D\left(x,y\right)}{D\left(u,v\right)}\right]\mathrm{d}u\mathrm{d}v,$$

(8.162)

其中 $\frac{D\left(x,y\right)}{D\left(u,v\right)},\frac{D\left(y,z\right)}{D\left(u,v\right)},\frac{D\left(z,x\right)}{D\left(u,v\right)}$ 和 $\mathrm{\Delta }$ 与前面的意义相同.

注 向量场理论一章讨论了向量值函数的曲面积分 (参见第 942 页 13.3.2).

8.5.3.2 曲面积分的性质

(1) 若积分区域即曲面 $S$ 能分成两部分 $S_1$ 和 $S_2$ (图 8.47),则

$${\int }_S\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right)={\int }_{S_1}\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right)$$$$\begin{array}{}\text{(8.163)}& +{\int }_{S_2}\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right).\end{array}$$

(2)若曲面改变方向, 即内外侧互换, 则积分变号:

$$\begin{array}{}\text{(8.164)}& {\int }_{S^{+}}\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right)=-{\int }_{S^{-}}\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right),\end{array}$$

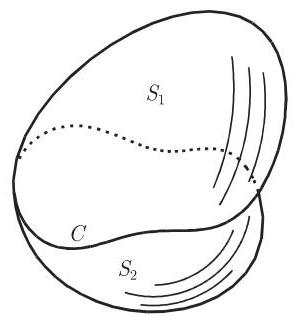
其中 $S^{+}$ 和 $S^{-}$ 表示同一曲面的两个不同方向.

(3) 通常曲面积分与曲面区域 $S$ 边界及曲面本身有关,因此对于由相同闭曲线 $C$ 张成的两个不同的非闭曲面区域 $S_1$ 和 $S_2$ ,它们的积分往往不同 (图 8.47):

$$\begin{array}{}\text{(8.165)}& {\int }_{S_1}\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right)\ne {\int }_{S_2}\left(P\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y\right).\end{array}$$

(4) 常用曲面积分来计算以闭曲面 $S$ 为边界的立体体积 $V$ ,积分计算公式如

下:

$$\begin{array}{}\text{(8.166)}& V=\frac{1}{3}{\int }_S\left(x\mathrm{d}y\mathrm{d}z+y\mathrm{d}z\mathrm{d}x+z\mathrm{d}x\mathrm{d}y\right),\end{array}$$$$\begin{array}{}\text{(8.167a)}& V={\int }_{S}x\mathrm{d}y\mathrm{d}z\text{ 或 }V={\int }_{S}y\mathrm{d}z\mathrm{d}x\text{ 或 }V={\int }_{S}z\mathrm{d}x\mathrm{d}y\text{ 或 }\end{array}$$$$\begin{array}{}\text{(8.167b)}& V=\frac{1}{3}{\int }_S\left(x\mathrm{d}y\mathrm{d}z+y\mathrm{d}z\mathrm{d}x+z\mathrm{d}x\mathrm{d}y\right),\end{array}$$

其中 $S$ 是使得外侧为正的有向曲面.

$◼$ 由球面公式 $x^2+y^2+z^2=R^2$ ,要想计算球体体积 $V$ ,需要利用球坐标 $x=$ $R\sin \vartheta \cos \phi ,y=R\sin \vartheta \sin \phi ,z=R\cos \vartheta \left(0\le \vartheta \le \pi ,0\le \phi \le 2\pi \right)$ 以及如 (8.160a) 中那样的雅可比行列式

$$\begin{array}{}\text{(8.168a)}& \frac{D\left(x,y\right)}{D\left(\vartheta ,\phi \right)}=\left|\begin{array}{ll}{x}_{\vartheta }& x_{\phi }\\ y_{\vartheta }& y_{\phi }\end{array}\right|=R^2\cos \vartheta \sin \vartheta .\end{array}$$

由(8.167a)中第三个积分,有

$$\begin{array}{}\text{(8.168b)}& V={\int }_{\phi =0}^{2\pi }{\int }_{\vartheta =0}^{\pi }{R}^3{\cos }^2\vartheta \sin \vartheta \mathrm{d}\vartheta \mathrm{d}\phi =2\pi R^3{\int }_0^{\pi }{\cos }^2\vartheta \sin \vartheta \mathrm{d}\vartheta =\frac{4}{3}\pi R^3.\end{array}$$